Формула довжини дуги кола: визначення, застосування та практичні приклади
Формула довжини дуги кола є фундаментальною концепцією в геометрії, яка знаходить широке застосування як у теорії, так і в практичних завданнях. Дуга — це частина кола, і її довжина залежить як від радіуса, так і від кута, що центрально перетинає цю дугу.
Основи та визначення
Перед тим як розглянути формулу довжини дуги кола, необхідно зрозуміти деякі ключові поняття:
- Коло: множина всіх точок на площині, що знаходяться на однаковій відстані від заданої точки (центру).
- Радіус: відстань від центру кола до будь-якої точки на колі.
- Кут: вимірюється у радіанах або градусах і є частиною, що утворюється двома радіусними лініями, які виходять з центральної точки до дуги.
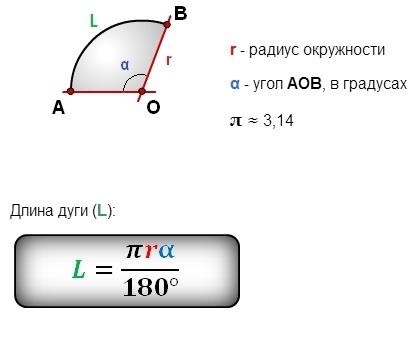
Виведення формули
Розглянемо, як працює формула довжини дуги кола. Довжина дуги (L) безпосередньо залежить від кута (θ) у радіанах і радіуса (r) кола:
| Параметр | Означення |
|---|---|
| θ | Кут у радіанах |
| r | Радіус кола |
| Formula | L = r * θ |
Для переведення кута з градусів у радіани використовується простий коефіцієнт перетворення: 1 радіан = 180/π градусів.
Застосування у практиці
Формула довжини дуги кола має широке застосування:
- У архітектурі і будівництві: для проектування круглих конструкцій, арок, мостів тощо.
- У механіці: для розрахунку траєкторій руху об’єктів, які рухаються по circular або чашовидним траєкторіям.
- У дизайні: створення графічних елементів та моделей, що потребують точних кривих.
Для прикладу розглянемо сценарій: вам потрібно знайти довжину дуги колеса, коли відомо, що радіус колеса становить 2 метри, а центральний кут — 30 градусів. Спочатку перетворимо кут у радіани: 30 градусів * (π/180) = π/6 радіан. Тепер підставимо значення у формулу: L = 2 * (π/6) ≈ 1.047 метрів.
Висновок
Розуміння і вміння застосовувати формулу довжини дуги кола є важливим навиком для спеціалістів у багатьох областях. Знання про те, як розрахувати довжину дуги, дозволяє виконувати складні проекти, що потребують точності й знань у геометрії. Формула довжини дуги кола, яка включає в себе лише радіус і центральний кут, є ключем до розв’язання широкого спектра завдань.