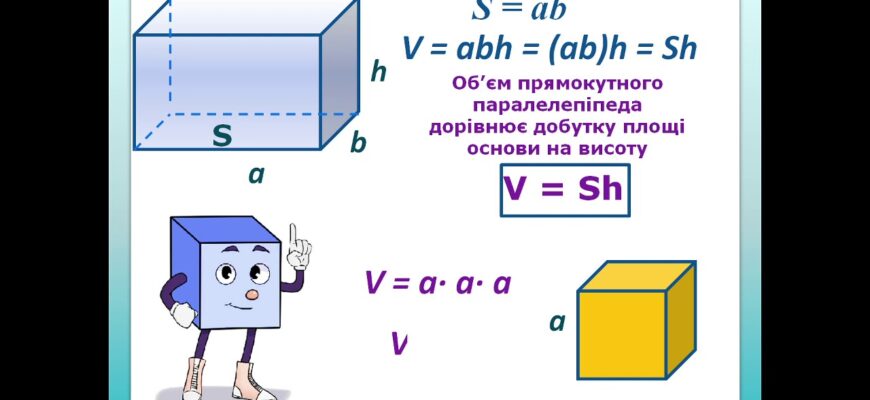
Формула об’єму прямокутного паралелепіпеда: основи та застосування
Формула об’єму прямокутного паралелепіпеда є фундаментальною у геометрії та знаходженні об’ємів різноманітних тривимірних тіл. Цей простий, але водночас потужний математичний засіб використовується не тільки в навчальних закладах, але й у багатьох галузях інженерії, архітектури та фізики.
Що таке прямокутний паралелепіпед?
Прямокутний паралелепіпед — це тривимірне геометричне тіло, грані якого є прямокутниками. Це тіло має шість граней, 12 ребер і вісім вершин. Назва “прямокутний” вказує на те, що всі ребра, які стикаються в кожній з вершин, утворюють прямий кут. Це означає, що всі границі цього паралелепіпеда є ортогональними одна до одної.
Як знайти об’єм прямокутного паралелепіпеда?
Формула об’єму прямокутного паралелепіпеда виглядає наступним чином:
V = a × b × c
де:
- V — об’єм паралелепіпеда
- a, b, c — довжини сторін, які утворюють три виміри тіла
Практичне застосування формули
Давайте розглянемо кілька прикладів, як можна застосовувати цю формулу у різних сферах життя:
- Будівництво: Архітектори та інженери використовують цю формулу для розрахунку об’ємів бетонних блоків або інших будівельних матеріалів.
- Пакування: В логістиці важливо знати, як багато коробок певного розміру можна вмістити у вантажний відсік.
- Виробництво: Знання об’єму допомагає визначити кількість сировини, необхідну для виробництва конкретних виробів.
Значення кожного параметра
Ключ до правильної інтеграції формули об’єму прямокутного паралелепіпеда в розрахунки полягає у точному визначенні довжин сторін a, b та c. Ось кілька важливих моментів:
| Параметр | Опис |
|---|---|
| a | Довжина однієї з граней паралелепіпеда. Це може бути основа будівлі або довжина контейнера. |
| b | Ширина паралелепіпеда. Це може бути ширина бетонного блоку або контейнера. |
| c | Висота паралелепіпеда. Важливо для розрахунку об’ємів рідин або сипких матеріалів. |
Техніка безпеки та обмеження
Використовуючи формулу об’єму прямокутного паралелепіпеда, необхідно враховувати, що:
- Всі виміри повинні бути в одній і тій же одиниці, щоб уникнути неправильних обчислень.
- Неточні виміри можуть призвести до значних відхилень в розрахунках, що може бути критичним у будівництві.
- Обчислення можуть бути ускладнені, якщо паралелепіпед складається з різних матеріалів, які мають різні властивості.