Формула об’єму циліндра: Поглиблене пояснення
Формула об’єму циліндра є фундаментальною складовою математичної геометрії та знаходиться в центрі уваги, коли мова йде про обрахунки в реальному житті. Хоча на перший погляд вона може здатися простою, її застосування поширюється на багато галузей, включаючи інженерію, архітектуру та виробництво.
Що таке циліндр
Циліндр — це геометричне тіло, яке складається з двох паралельних круглих основ, з’єднаних бічною поверхнею. Важливо розуміти базові складові циліндра, щоб правильно застосувати формулу об’єму:
- Радіус основи (r) — відстань від центру кола до його краю.
- Висота (h) — перпендикулярна відстань між двома основами.
- Основа — коло, яке визначає форму перетину циліндра.
Формула об’єму циліндра
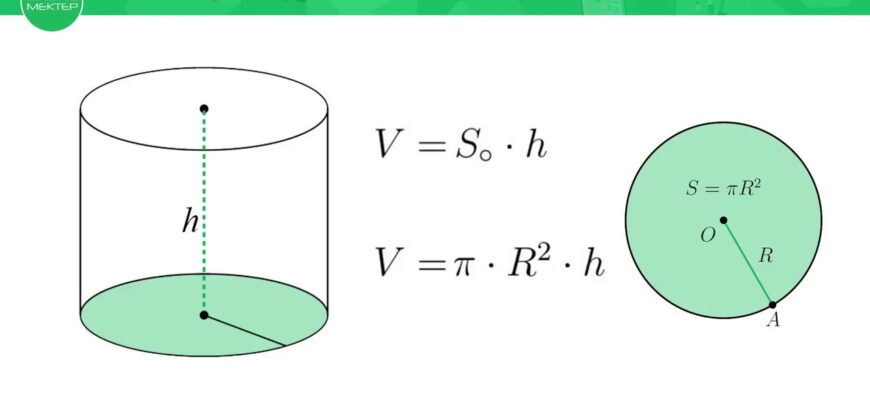
Формула об’єму циліндра виглядає так:
V = πr2h
- Де V — об’єм циліндра,
- π — математична константа, приблизно рівна 3.14159,
- r — радіус основи,
- h — висота циліндра.
Розуміння та застосування формули
Для практичного застосування формули об’єму циліндра важливо враховувати розмір та одиниці вимірювання, оскільки неправильний підхід може призвести до значних помилок в обчисленнях. Розглянемо декілька прикладів використання:
| Сфера застосування | Приклад |
|---|---|
| Інженерія | Проектування резервуарів для рідини, де обʼєм циліндра використовується для вимірювання ємності. |
| Архітектура | Створення дизайнів колон і подібних структурних елементів. |
| Виробництво | Розрахунок матеріалів для виготовлення труб, контейнерів, банок тощо. |
Ключові аспекти обчислення
- Точність вимірювань: Для досягнення точного результату важливо мати точні виміри радіуса та висоти.
- Одиниці виміру: Завжди переконуйтесь, що радіус та висота вимірюються в одних і тих самих одиницях, щоб уникнути розбіжностей в обчисленнях.
- Перетворення одиниць: Іноді може знадобитися перетворення одиниць виміру (наприклад, з сантиметрів в метри), щоб відповідати стандартам задачі або проекту.
Висновок
Формула об’єму циліндра, V = πr2h, є універсальним інструментом, завдяки якому можна розрахувати об’єм циліндричних об’єктів в різноманітних галузях. Успішне застосування формули у великій мірі залежить від точності вимірювань та правильності обчислень. Враховуючи всі означені аспекти, ви зможете ефективно використовувати ці знання у професійній діяльності та повсякденному житті.