Формула Площі Трапеції: Основи та Особливості
Формула площі трапеції є незамінним інструментом у геометрії та часто використовується для розв’язання задач, пов’язаних з вимірюванням площ різних фігур. Трапеція — це чотирикутник, у якого дві протилежні сторони паралельні, і для знаходження її площі існує кілька підходів. Але найпоширеніший з них базується саме на базовій формулі.
Основна Формула Площі Трапеції
Формула площі трапеції виглядає наступним чином:
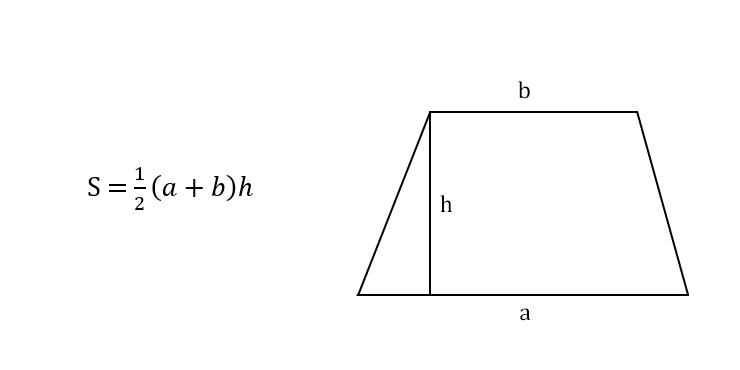
S = 0.5 × (a + b) × h
- S — площа трапеції
- a та b — довжини паралельних сторін
- h — висота трапеції (перпендикулярна відстань між паралельними сторонами)
Ця формула є досить простою для використання, якщо ви знаєте довжини двох основ трапеції та висоту. Питання може виникнути лише у випадку, якщо одне з цих значень відсутнє. У такому випадку потрібно буде скористатися додатковими методами обчислення висоти чи основ, використовуючи інші властивості трапеції.
Варіанти Обчислення Площі Трапеції
Існує кілька підходів до обчислення площі трапеції, залежно від відомих величин:
- Через формулу площі трапеції: Якщо відомі довжини обох паралельних сторін і висота, використовують основну формулу S = 0.5 × (a + b) × h.
- Через діагоналі: Якщо відомі діагоналі трапеції і кут між ними, можна використовувати іншу формулу: S = 0.5 × d1 × d2 × sin(θ), де d1 та d2 — діагоналі, а θ — кут між ними.
- Через середню лінію: Середня лінія трапеції дорівнює півсумі її основ, отже можна використовувати формулу: S = m × h, де m — середня лінія.
Практичні Приклади
| Приклад | Дані | Обчислення |
|---|---|---|
| Приклад 1 | a = 6 см, b = 10 см, h = 4 см | S = 0.5 × (6 + 10) × 4 = 32 см² |
| Приклад 2 | Через середню лінію, m = 8 см, h = 5 см | S = 8 × 5 = 40 см² |
Чому Знати Формулу Важливо
Формула площі трапеції відіграє важливу роль в різних дисциплінах, включаючи архітектуру, дизайн та навіть у астрономії. Вміння швидко обчислювати площу трапеції допомагає у вирішенні практичних задач та підвищує загальну математичну грамотність.
Узагальнюючи, можна сказати, що формула площі трапеції — це один із найважливіших елементів у геометрії. Знання її використання допомагає розширити геометричну інтуїцію та практичні навички вирішення математичних проблем.