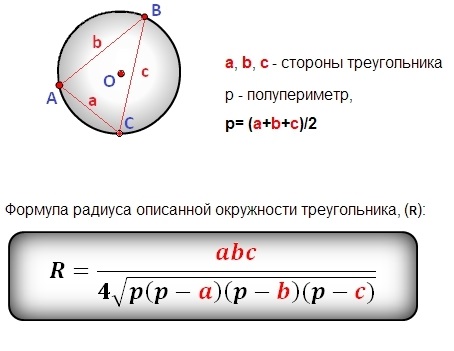
Формула радіуса описаного кола
Формула радіуса описаного кола дозволяє обчислити радіус кола, яке проходить через усі вершини даного трикутника. Цей розрахунок має важливе значення у геометрії та знаходить застосування в різних практичних задачах, таких як навігація, архітектура та інженерія.
Вступ у тему
У геометрії, описане коло трикутника — це коло, що проходить через усі три його вершини. Центр цього кола називається центроїдом трикутника, а радіус — радіусом описаного кола.
Важливість знання формули
Знання та застосування формули радіуса описаного кола допомагає:
- Відкривати нові властивості трикутників.
- Розв’язувати задачі з геометрії на конкурсах та олімпіадах.
- Полегшити процес побудови геометричних фігур у різноманітних практичних завданнях.
Формула
Основна формула радіуса описаного кола трикутника задається формулою:
R = (a * b * c) / (4 * S)
де R — це радіус описаного кола, a, b, та c — довжини сторін трикутника, а S — площа трикутника.
Супутні формули
Щоб знайти площу трикутника, можна скористатися формулою Герона:
S = √(p * (p-a) * (p-b) * (p-c))
де p — півпериметр трикутника:
p = (a + b + c) / 2
Приклад обчислень
- Знайдіть довжини сторін трикутника: a = 5, b = 6, c = 7.
- Обчисліть півпериметр: p = (5 + 6 + 7) / 2 = 9.
- Обчисліть площу трикутника за формулою Герона:
S = √(9 * (9-5) * (9-6) * (9-7)) = √(9 * 4 * 3 * 2) = √216 = 14.7 (приблизно). - Обчисліть радіус описаного кола:
R = (5 * 6 * 7) / (4 * 14.7) = 210 / 58.8 = 3.57 (приблизно).
Значення та застосування
Формула радіуса описаного кола є ключовим інструментом геометрії, який знаходить застосування в багатьох областях. Її можна використовувати для вивчення властивостей різних трикутників, їх форми та розташування в просторі.
| Сфера | Застосування |
|---|---|
| Навігація | Використовується для визначення маршруту, розрахунку відстаней. |
| Архітектура | Розрахунок параметрів конструкцій, в яких використовуються трикутні елементи. |
| Інженерія | Проектування деталей з трикутними отворами або елементами. |
Таким чином, формула радіуса описаного кола не тільки лежить в основі багатьох теоретичних відкриттів, але й забезпечує практичне застосування, що робить її важливою для будь-кого, хто займається геометрією чи суміжними дисциплінами.