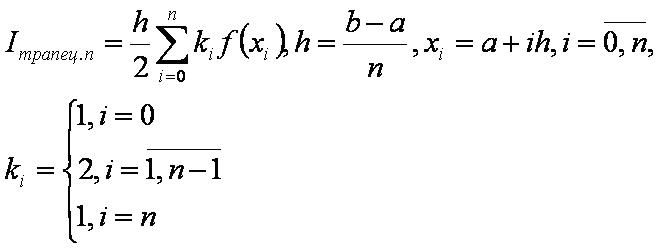Формула трапеций
Формула трапеций є одним з важливих методів чисельного інтегрування, який широко застосовується в математичному аналізі та прикладних науках для обчислення певних інтегралів. Цей метод пропонує оптимальне співвідношення між точністю та обчислювальними ресурсами, що робить його особливо привабливим для великих обчислень.
Основи методу трапеций
Метод трапеций базується на наближенні кривої функції прямолінійними відрізками або трапеціями, з яких складається певний інтервал інтегрування. Основна ідея полягає в тому, щоб замінити криву функції на певному інтервалі на послідовність трапецій, і сумарна площа цих трапецій наближено дорівнює значенню інтеграла функції.
Формула трапеций для обчислення певного інтегралу виглядає наступним чином:
| Обозначення | Опис |
|---|---|
| a | початкова точка інтервалу інтегрування |
| b | кінцева точка інтервалу інтегрування |
| n | кількість елементів розбиття інтервалу |
| h | довжина кроку: ( h = frac{b-a}{n} ) |
Формула трапеций має вигляд:
Т = (frac{h}{2}) [f(a) + 2f(a + h) + 2f(a + 2h) + … + 2f(b – h) + f(b)]
Переваги та недоліки методу трапеций
Переваги
- Простота реалізації та застосування.
- Застосовність до широкого класу функцій.
- Забезпечує гарний баланс між точністю і швидкістю обчислень.
Недоліки
- Обмежена точність для функцій з великими змінами або різкими скачками.
- Вимагає збільшення кількості інтервалів для підвищення точності, що може бути обчислювально затратним.
Приклади застосування
Розглянемо приклад, коли необхідно обчислити інтеграл функції f(x) = x^2 на інтервалі [0, 2]. Використання методу трапеций для чотирьох підінтервалів (n=4) може бути зображено наступним чином:
- Обчислення довжини кроку: ( h = frac{2-0}{4} = 0.5 ).
- Застосування формули трапеций:
- ( T = frac{0.5}{2} [f(0) + 2f(0.5) + 2f(1.0) + 2f(1.5) + f(2)] )
- ( T = 0.25 [0 + 2(0.25) + 2(1.0) + 2(2.25) + 4] )
- ( T = 0.25 [0 + 0.5 + 2 + 4.5 + 4] )
- ( T = 0.25 [11] = 2.75 )
Згідно з аналітичними розрахунками, інтеграл функції на цьому інтервалі дорівнює (frac{8}{3}), тобто приблизно 2.67. Як бачимо, метод трапеций дає наближене значення з невеликою похибкою.
Заключення
Формула трапеций є цінним інструментом для обчислення певних інтегралів, особливо коли аналітичний підхід неможливий або складний. Завдяки своїй простоті та гнучкості, цей метод широко використовується в інженерних розрахунках, фізичних моделях і інших галузях, де важливі швидкість і ефективність обчислень.
