Об’єм прямокутного паралелепіпеда: формула і приклади
Об’єм прямокутного паралелепіпеда — це ключовий математичний параметр, що характеризує просторовий розмір цього геометричного тіла. Об’єм прямокутного паралелепіпеда формула дозволяє обчислити цю величину з використанням лінійних розмірів фігури. Це знання необхідне як у математиці, так і в багатьох областях науки та техніки. Розглянемо детальніше цю тему та звернемо увагу на методи обчислення, практичні приклади і застосування в реальному житті.
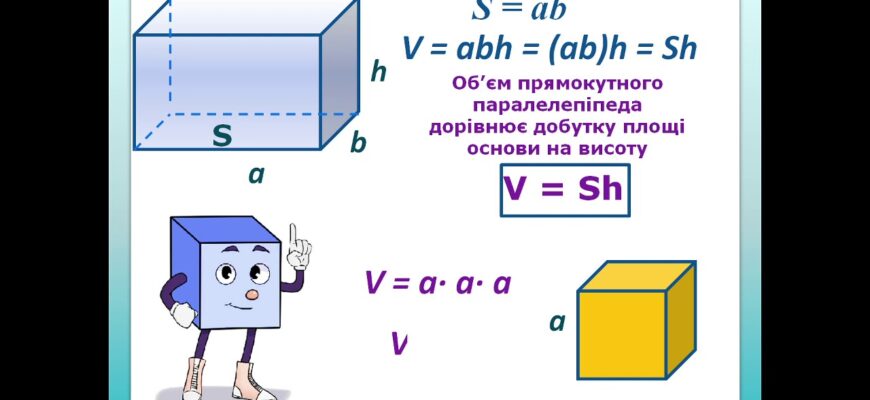
Формула об’єму прямокутного паралелепіпеда
Об’єм прямокутного паралелепіпеда визначається як добуток трьох його вимірів — довжини (a), ширини (b) та висоти (h). В такому випадку математичний вираз для розрахунку виглядає наступним чином:
| Формула об’єму |
|---|
| V = a × b × h |
Де V — це об’єм прямокутного паралелепіпеда, a — довжина, b — ширина, а h — висота. Зазвичай цей об’єм вимірюється в кубічних одиницях, відповідно до вибору одиниць вимірювань для a, b та h. Це можуть бути, наприклад, кубічні сантиметри, метри чи інші одиниці об’єму.
Застосування формули в практиці
У багатьох випадках, обчислення об’єму прямокутного паралелепіпеда є необхідним для вирішення практичних задач:
- Будівництво та архітектура: Розрахунок об’єму матеріалів, необхідних для заповнення певного простору, наприклад, бетону для фундаменту.
- Логістика: Визначення об’єму коробки для транспортування певного вантажу.
- Виробництво: Розрахунки необхідні для належного пакування товарів у задану коробку.
Приклад розрахунку об’єму
Розглянемо приклад практичного застосування об’єм прямокутного паралелепіпеда формули. Припустимо, що потрібно знайти об’єм коробки з такими розмірами:
- Довжина a = 2 метри
- Ширина b = 1.5 метри
- Висота h = 1 метр
Обчислюємо об’єм за формулою:
| V | = 2 × 1.5 × 1 = 3 кубічних метра |
Таким чином, об’єм цієї коробки становить 3 кубічні метри.
Click here to preview your posts with PRO themes ››
Висновок
Об’єм прямокутного паралелепіпеда формула є важливим інструментом для обчислення просторових характеристик цієї геометричної фігури. Використовуючи просту математичну операцію множення, можна легко отримати потрібний результат, що робить цю формулу надзвичайно корисною в багатьох галузях діяльності, від науки до повсякденного життя. Маючи уявлення про обчислення об’єму, ми можемо ефективніше планувати та реалізовувати різноманітні задачі, що спрощує безліч практичних ситуацій і оптимізує використання ресурсів.
