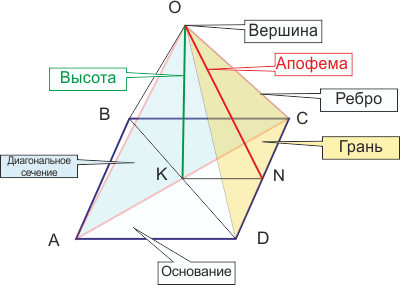
Апофема це: розуміння основного геометричного елемента
Апофема це термін з геометрії, який часто використовується в контексті вивчення правильних багатокутників та кіл. За своєю суттю, апофема є відстанню від центру багатокутника до середини будь-якої його сторони. Апофема тісно пов’язана з радіусом вписаного круга і має безліч практичних застосувань в реальному світі. В даній статті ми розглянемо концепцію апофеми, її властивості, формули та значення в геометрії та суміжних науках.
Властивості апофеми
- Геометричне визначення: Апофема правильної фігури є перпендикуляром, що спускається з центру фігури на одну зі сторін.
- Для правильних багатокутників: Апофема завжди є перпендикулярною до сторони.
- Зв’язок із вписаним кругом: Довжина апофеми дорівнює радіусу круга, вписаного в правильний багатокутник.
Обчислення апофеми
Для розрахунку апофеми існують спеціальні формули, залежні від типу багатокутника. Наприклад, для правильного n-кутника зі стороною a, апофема (A) може визначатися за допомогою тригонометричних функцій:
A = frac{a}{2 cdot tan(pi/n)} Ця формула виводиться з трикутників, утворених радіусами вписаного круга та апофемами. Дане рівняння дозволяє досить точно обрахувати довжину апофеми для правильних багатокутників.
Практичне застосування апофеми
- У будівництві: Апофема допомагає у проектуванні структур, пов’язаних з багатокутниками, таких як дахи або куполи.
- У мистецтві: Для створення узорів і вітражів, де часто використовуються правильні багатокутники.
- У математиці: Апофема використовується у формування теорем та задач, що стосуються багатокутників.
Порівняльна таблиця значення апофеми
| Тип багатокутника | Сторона (a) | Кількість сторін (n) | Апофема (A) |
|---|---|---|---|
| Трикутник | a | 3 | (A = frac{a}{2 cdot tan(pi/3)}) |
| Квадрат | a | 4 | (A = frac{a}{2 cdot tan(pi/4)}) |
| П’ятикутник | a | 5 | (A = frac{a}{2 cdot tan(pi/5)}) |
Висновки
Розглядаючи апофема це, ми бачимо, що вона є важливим елементом у геометрії. Вона представляє собою фундаментальний концепт, без якого складно уявити собі вивчення правил та властивостей правильних багатокутників. Розуміння того, як обчислюється і застосовується апофема, може полегшити рішення багатьох геометричних завдань і активізувати використання цієї характеристики у практичних завданнях, як-от архітектурних або дизайнерських проектах.