Що таке діаметр кола: Основи геометрії
Що таке діаметр кола – це одне з фундаментальних понять у геометрії, яке відіграє важливу роль в багатьох галузях науки і техніки. Уявімо круг, одну з основних геометричних фігур, з якою ми знайомимося ще в дитинстві. Його діаметр є ключовим параметром, що описує його основні властивості.
Основне визначення діаметра кола
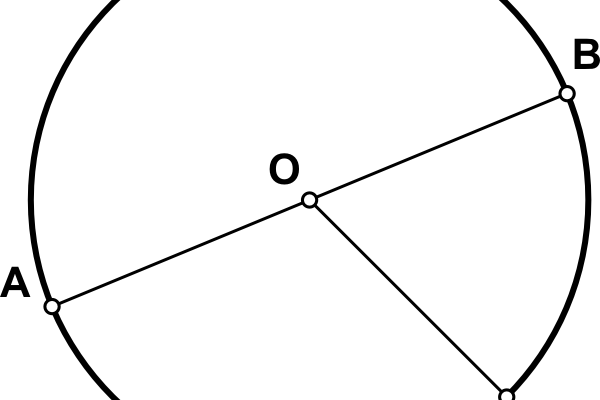
Діаметр кола – це відрізок, що проходить через центр кола і з’єднує дві точки на його периферії. Іншими словами, діаметр є найдовшою відстанню між двома точками на колі, яку можна протягнути в середині кола. Варто зазначити, що діаметр завжди подвоєний радіус, тобто:
Формула:
| Позначення | Формула |
|---|---|
| Діаметр (D) | D = 2r, де r – радіус кола |
Властивості діаметра
- Центральне положення: Діаметр завжди проходить через центр кола, розділяючи його на дві рівні частини – напівколо.
- Поділ кола: Кожен діаметр поділяє коло на дві однакові, симетричні частини.
- Основа для обчислень: Діаметр використовується для обчислення довжини кола, площі круга та інших геометричних властивостей.
Де використовують знання про діаметр
- Будівництво та архітектура: Діаметри круглих архітектурних елементів — наприклад, арок або куполів.
- Інженерія: Діаметри труб, валів та інших циліндричних об’єктів.
- Астрономія: Обчислення діаметрів планет або орбіт небесних тіл.
- Медицина: Використовується при обчисленні діаметрів кровоносних судин та різних медичних інструментів.
Взаємозв’язок з іншими геометричними поняттями
Діаметр кола є основою для вивчення інших геометричних понять, таких як радіус, довжина кола, площа круга та центральний кут. Всі ці властивості є взаємопов’язаними, і зміна одного параметра завжди впливає на інші.
Приклад: Довжина кола (периметр кола) визначається формулою: L = πD, де D – діаметр, а π (пі) – математична константа, приблизно рівна 3.14159.
Заключення
У підсумку, розуміння, що таке діаметр кола, є критично важливим для багатьох областей науки і повсякденного життя. Знання і використання цього поняття дозволяє точно описувати та обчислювати властивості круглих об’єктів, роблячи наші розрахунки більш точними і зрозумілими.