Формула синусів: теоретичні засади та практичне застосування
Формула синусів є фундаментальним засобом у тригонометрії, яка дозволяє зв’язати масштаби елементів трикутника з їхніми кутами. Це універсальний підхід для вирішення різноманітних тригонометричних задач, що робить її незамінною в геометрії та інших прикладних науках.
Теорема синусів: сутність і доказ
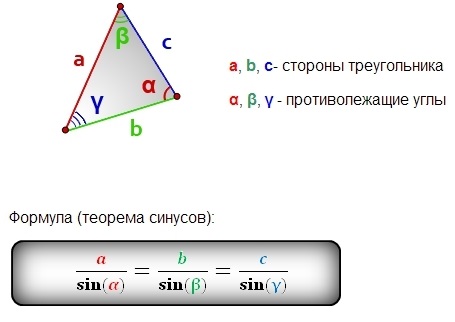
Теорема синусів (або формула синусів) стверджує, що у будь-якому трикутнику відношення довжини сторони трикутника до синуса протилежного кута є незмінною величиною, тобто дорівнює діаметру описаного кола. Це виражається наступним чином для трикутника ABC:
| Сторона | Синус кута | Відношення |
|---|---|---|
| a | sin(α) | a / sin(α) = 2R |
| b | sin(β) | b / sin(β) = 2R |
| c | sin(γ) | c / sin(γ) = 2R |
Де a, b, c — сторони трикутника, α, β, γ — відповідні кути, а R — радіус кола, описаного навколо трикутника.
Доказ теореми
- Перетворення трикутника ABC у рівносторонній для простоти розрахунків.
- Розрахунок відстаней між вершинами, заснований на тригонометричних функціях:
a = 2Rsin(α), b = 2Rsin(β), c = 2Rsin(γ). - Отримання остаточної формули:
a/sin(α) = b/sin(β) = c/sin(γ) = 2R.
Застосування формули синусів
Формула синусів широко використовується у різних галузях, включаючи:
- **Геодезія**: Для обчислення відстаней і кутів під час картографічних робіт.
- **Астрономія**: У вимірюванні відстаней між небесними об’єктами.
- **Будівництво**: При проектуванні складних конструкцій.
Приклади застосування
Розглянемо задачу для практичного застосування формули. Нехай нам відомі одна сторона і два кути у трикутнику. Як обчислити невідомі елементи?
Наприклад, відомо a = 7 см, α = 30°, і β = 45°. Потрібно знайти b і c.
Застосовуючи формулу:
- Знаходимо c, розрахувавши γ:
γ = 180° – α – β = 105°. - Застосуємо формулу:
b = a * sin(β) / sin(α). - Обчислюємо:
b ≈ 7 * sin(45°) / sin(30°) ≈ 9.899 см. - Для c використовуємо:
c = a * sin(γ) / sin(α). - Обчислюємо:
c ≈ 7 * sin(105°) / sin(30°) ≈ 12.124 см.
Підсумовуючи, формула синусів забезпечує ефективний підхід до вирішення багатьох практичних задач, де вона допомагає знаходити як великі, так і малі елементи трикутника. Знання цієї формули є надзвичайно корисним для математиків, інженерів, архітекторів і багатьох інших професіоналів.