Многокутник це: Вступ до геометрії
Многокутник це основне поняття в геометрії, яке відоме ще з часів античних математиків. Поняття “многокутник” охоплює фігури, які мають багато вершин і сторін. Це універсальне поняття включає трикутники, чотирикутники, п’ятикутники і т.д., до безкінечності. У цій статті ми розглянемо властивості та особливості многокутників, їх застосування, а також деякі цікаві факти, які допоможуть краще зрозуміти цю геометричну концепцію.
Основні властивості многокутників
Многокутники мають кілька характеристичних властивостей, що визначають їх форму та структуру:
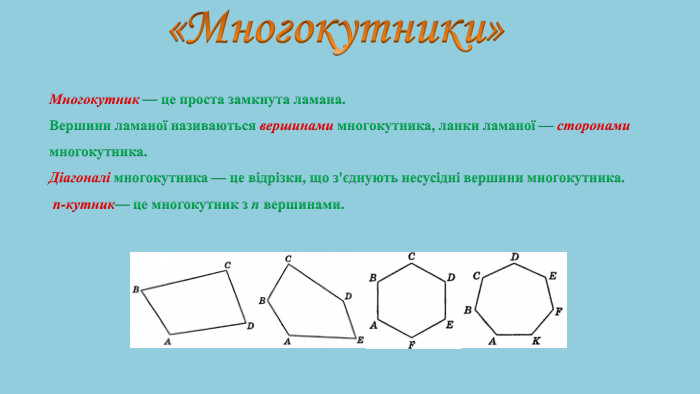
- Сторони: Многокутник складається з відрізків, які називаються сторонами.
- Вершини: Точки, де сторони між собою з’єднуються, є вершинами многокутника.
- Кути: Кути формуються на перетині сторін у вершинах.
Типи многокутників
Многокутник це не просто класифікація фігур за кількістю сторін, а й за формою і властивостями. Розглянемо деякі найпоширеніші типи многокутників:
- Описані многокутники: У них усі вершини лежать на одній окружності.
- Правильні многокутники: Це фігури, де всі сторони і кути рівні. Класичний приклад — правильний трикутник.
- Впорядковані многокутники: У них сторони можуть бути різної довжини, але вони вписані у правильний порядок.
Формули і розрахунки
Говорячи про многокутники, важливо знати основні формули для розрахунку периметрів і площ.
| Тип многокутника | Формула для периметра | Формула для площі |
|---|---|---|
| Трикутник | P = a + b + c | A = 0.5 * база * висота |
| Чотирикутник | P = a + b + c + d | A = довжина * ширина (для прямокутника) |
| Правильний многокутник | P = n * a | A = (n * a^2) / (4 * tan(π/n)) |
Застосування многокутників
- Архітектура: Многокутники використовуються в дизайні будівель і споруд для надання їм стійкості та естетичної привабливості.
- Інженерія: Розрахунки многокутників важливі для проектування деталей машин та механізмів.
- Комп’ютерна графіка: Багатокутники лежать в основі моделей 3D-графіки, використовуючи полігони для створення реалістичних об’єктів.
Цікаві факти про многокутники
Многокутники не лише основа геометрії, це ще й багатовіковий інструмент, який допомагав у розвитку математики:
- Перші згадки про многокутники зустрічаються ще в працях Піфагора.
- Кількісну властивість многокутника вписаної у нього окружності активно використовували у дослідженнях давньогрецьких вчених.
- Відомий математик і філософ Архімед часто використовував многокутники для підрахунку площ та періметра форм.
Многокутник: Висновки
Отже, многокутник це не просто набір точок і ліній на площині, а концепція, яка стала важливою частиною математики та архітектури. Від його базових характеристик до численних застосувань у нашому повсякденному житті — многокутник залишається ключовим елементом багатьох наукових досягнень. Наступного разу, коли ви побачите многокутник у своїм оточенні, пам’ятайте про його багатогранність і важливість в нашому світі.