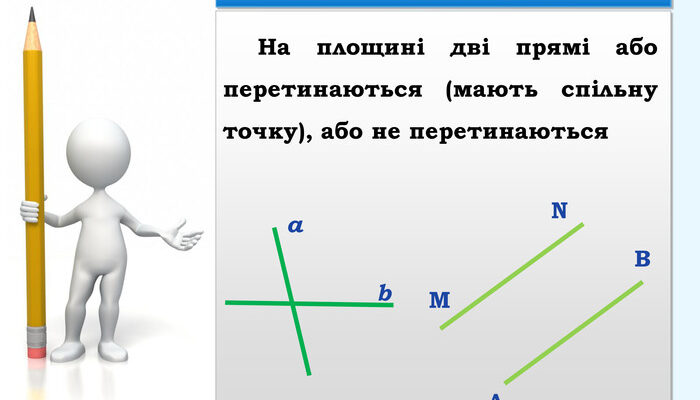
Що таке паралельні прямі
Що таке паралельні прямі? У геометрії під цим терміном розуміють дві або більше прямі, які лежать в одній площині і жодного разу не перетинаються, якими б довгими вони не були. Ці лінії зберігають постійну відстань одна від одної, тому ми можемо сказати, що вони йдуть “поруч”.
Властивості паралельних прямих
Основні властивості
- Неперетинання: Паралельні прямі ніколи не зустрінуться. Це означає, що в жодній точці вони не перетинаються.
- Рівнобіжність: Відстань між будь-якими двома точками на кожній з паралельних прямих залишається постійною.
- Однакова нахиленість: Якщо дивитися на графіки прямих в координатній площині, вони матимуть тотожний коефіцієнт нахилу.
- Геометрична конфігурація: Паралельні прямі зберігають пропорції у трикутнику, якщо вони є його частинами.
Символіка
У математиці для позначення паралельних прямих часто використовують символ ||. Наприклад, A || B читається як “пряма A паралельна прямій B”.
Способи визначення паралельності
- Перемірювання відстані: Якщо відстань між двома прямими однакова у всіх точках, вони є паралельними.
- Коефіцієнт нахилу: Якщо коефіцієнти нахилу двох прямих рівні, ці прямі паралельні.
- Власності кутів: У випадку, коли дві прямі перетинають третю пряму холеричність, кути, які утворюються, дають можливість визначити паралельність.
| Метод | Опис |
|---|---|
| Коефіцієнт нахилу | Якщо пряма з рівнянням y = mx + b має нахил m, то будь-яка інша пряма з тим же нахилом m буде паралельною. |
| Властивості кутів | В разі перетину паралельних прямих третьою прямою, відповідні кути є рівними. |
Приклади використання паралельних прямих
У щоденному житті ми часто зіштовхуємося з паралельними прямими без навіть особливого помічання. Ось декілька прикладів:
- Колії залізничного шляху, які йдуть паралельно одна одній.
- Сторони зошитів або книг, які є паралельними.
- Шляхові смуги на дорогах, які часто паралельні одна одній.
Заключення
Знання про те, що таке паралельні прямі, є основоположними у багатьох галузях науки та інженерії. Визначення паралельності дозволяє спростити рішення задач і проектування об’єктів. Ці знання також допомагають візуалізувати та розв’язувати складні геометричні проблеми. Завдяки чітким властивостям і методам визначення, паралельні прямі залишаються одним з найважливіших концептів в геометрії.