Що таке суміжні кути?
Питання “що таке суміжні кути” є одним із фундаментальних у планіметрії, розділі геометрії, що вивчає властивості плоских фігур. Суміжні кути виникають у процесі побудови та аналізу різних геометричних об’єктів, від прямих ліній до складних форм. Розуміння цих кутів важливо для математичного аналізу та вирішення прикладних задач.
Визначення та основні властивості
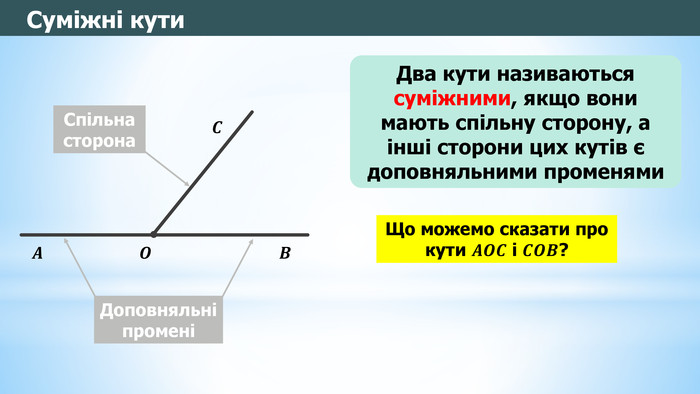
Суміжні кути – це два кути, які мають спільну вершину та одну спільну сторону, в той час як інші сторони цих кутів знаходяться на одній прямій, тобто утворюють зі спільною стороною піраміду. Існує кілька важливих властивостей, які характеризують суміжні кути:
- Сума суміжних кутів завжди дорівнює 180°. Це випливає з того, що прямі кути утворюють пряму лінію.
- Якщо один із суміжних кутів відомий, інший можна знайти, віднявши від 180° значення відомого кута.
Застосування в геометрії
Суміжні кути формують основу для вирішення багатьох задач у планіметрії. Вони використовуються для:
- Визначення невідомих величин у трикутниках і чотирикутниках.
- Аналізу взаємного розташування прямих на площині.
- Обчислення внутрішніх кутів багатокутників.
Наприклад, у багатокутниках, таких як квадрат або прямокутник, суміжні кути важливі для визначення пропорцій та симетрії.
Приклади задач з використанням суміжних кутів
Для кращого розуміння розглянемо приклад задачі на застосування властивостей суміжних кутів:
| Умова | Розв’язок |
|---|---|
| Відомо, що один із суміжних кутів дорівнює 45°. Знайдіть інший кут. | Інший кут дорівнює 180° – 45° = 135°. |
Ще один приклад ілюструє застосування суміжних кутів при обчисленні параметрів трикутників:
| Умова | Розв’язок |
|---|---|
| У трикутнику ABC ∠A має 60°, ∠B – 50°. Знайти ∠C. | Сума внутрішніх кутів трикутника дорівнює 180°. Тому, ∠C = 180° – (60° + 50°) = 70°. |
Практичне значення
Суміжні кути не тільки мають теоретичне значення в геометрії, але й знаходять практичне застосування у різних галузях, таких як архітектура, інженерія та комп’ютерна графіка. Коректне використання суміжних кутів дозволяє створювати точні креслення та моделі, забезпечуючи коректність та точність у реальних проєктах.
Отже, розуміння цього, що таке суміжні кути, є ключовим не лише для вирішення математичних задач, але й для успішної реалізації різноманітних проектів у діяльності людини, що вимагає точності та логічного мислення.