Теорема Фалеса: Від Теоретичного Перспективи до Практичного Застосування
Теорема Фалеса є однією з найдавніших і найвідоміших теорем у геометрії, що має значний вплив на розвиток математичної науки. Незважаючи на свій віковий вік, ця теорема має потужний вплив на сучасні математичні методи та їх практичне застосування. У цій статті ми розглянемо історію, формулювання й застосування теореми Фалеса в різних галузях.
Історичний Контекст
Теорема Фалеса є однією з найперших математичних теорем, що була сформульована давньогрецьким математиком і філософом Фалесом Мілетським в VI столітті до нашої ери. Вона стала одною з перших наукових спроб пояснити природу простору і форми у строгих аксіоматичних термінах. Ця теорема є одним із найяскравіших прикладів давньогрецької математичної думки, яка заклала основу для більш складних математичних концепцій.
Формулювання Теореми Фалеса
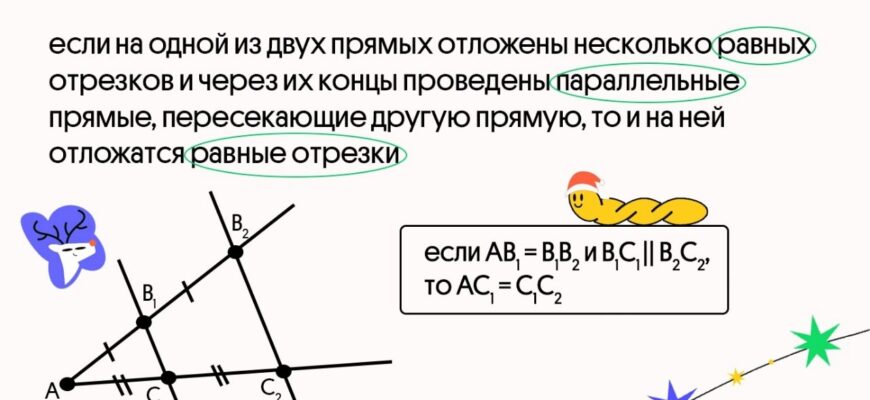
При описі теореми Фалеса, важливо врахувати, що вона базується на відношеннях у паралельних прямих і відрізках. Формально вона звучить наступним чином:
- Якщо дві паралельні прямі, що перетинають дві інші прямі, тоді відрізки, що створюються між цими перетинами на одній прямій, знаходяться у такому ж відношенні, як і відповідні відрізки на іншій прямій.
Це можна записати математично:
Якщо AB і CD є паралельними прямими, що перетинають AC і BD, то відношення AB:CD дорівнює AC:BD.
Доказ і Довідкові Висновки
Ця теорема легко доводиться за допомогою поняття подібності трикутників. Якщо ми розглянемо точки перетину прямої з паралельними прямими, то утворені трикутники є подібними, а це автоматично веде до рівності відношень відповідних сторін. Це базовий принцип, що лежить в основі складніших теорем у геометрії та алгебрі.
Застосування Теореми Фалеса
Теорема Фалеса має численні застосування у різних галузях науки та техніки. Вона лежить в основі багатьох систем обчислення, аналітичної геометрії та навіть компьютерної графіки. Ось кілька головних застосувань:
- Будівництво та Архітектура: Теорема Фалеса використовується для точного вимірювання і проектування лінійних структур і конструкцій.
- Інженерія: Теорема застосовується при проєктуванні механічних систем і розрахунку відстаней.
- Комп’ютерна Графіка: Візуалізація та рендеринг тривимірних об’єктів базуються на основних принципах теореми.
| Галузь | Застосування |
|---|---|
| Будівництво | Проєктування лінійних конструкцій |
| Інженерія | Проєктування механічних систем |
| Комп’ютерна графіка | Рендеринг тривимірних моделей |
Висновок
Теорема Фалеса не втрачає своєї важливості навіть у сучасному світі. Вона є основною ланкою між класичними та сучасними науковими дисциплінами, і багато в чому її дослідження продовжується шляхом інтеграції у нові технології та області знань. Теорема вирізняється своєю простотою, але водночас і глибиною, що дозволяє використовувати її в широкому діапазоні практичних застосувань у сучасному світі.