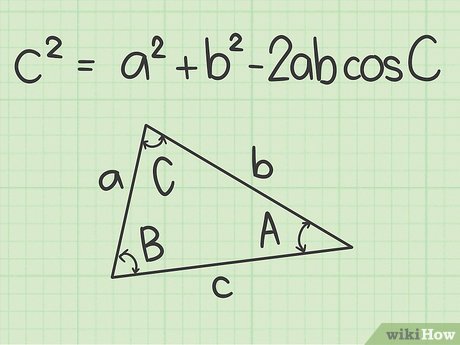
Теорема косинусів: формула і її застосування
Теорема косинусів, формула якої є важливим елементом у геометрії, зокрема в тригонометрії, використовує співвідношення між сторонами трикутника і косинусом одного з його кутів. Це незамінний інструмент у випадках, коли неможливо застосувати теорему Піфагора, оскільки мова йде про трикутники, які не є прямокутними.
Що таке теорема косинусів?
Теорема косинусів: у будь-якому трикутнику квадрат довжини однієї сторони дорівнює сумі квадратів довжин двох інших сторін мінус подвоєний добуток довжин цих сторін на косинус кута між ними.
Формально це виражається таким чином:
- a2 = b2 + c2 – 2bc * cos(α)
- b2 = a2 + c2 – 2ac * cos(β)
- c2 = a2 + b2 – 2ab * cos(γ)
Застосування теореми косинусів
У яких випадках застосовується теорема косинусів?
- Коли відомі довжини трьох сторін трикутника, але необхідно знайти один із кутів.
- Коли відомі дві сторони трикутника та кут між ними, але потрібно знайти третю сторону.
Приклади вирішення задач з використанням теореми косинусів
Розглянемо приклад, коли відомі дві сторони і кут між ними:
Дано трикутник ABC, де:
| Сторона | Довжина |
|---|---|
| AB | 8 см |
| AC | 6 см |
Кут A = 60°. Знайти сторону BC.
Використовуючи формулу:
BC2 = AB2 + AC2 – 2 * AB * AC * cos(A)
Підставляємо значення:
BC2 = 82 + 62 – 2 * 8 * 6 * cos(60°)
BC2 = 64 + 36 – 96 * 0.5 = 64 + 36 – 48 = 52
BC = √52 ≈ 7.21 см
Навіщо використовувати теорему косинусів?
- Теорема косинусів дозволяє знайти невідомі величини в трикутнику без необхідності прямих вимірювань.
- Ця теорема розширює можливості геометрії поза межами прямокутних трикутників.
- Вона допомагає в знаходженні рішення, коли інші методи є недоступними або неефективними.
Таким чином, теорема косинусів, формула якої проста в застосуванні, служить потужним інструментом у вирішенні складних геометричних задач, допомагаючи інженерам, архітекторам і науковцям проводити складні розрахунки. Вона забезпечує надійний спосіб обчислень у трикутниках, які не є прямокутними, і таким чином розширює традиційні межі тригонометрії.