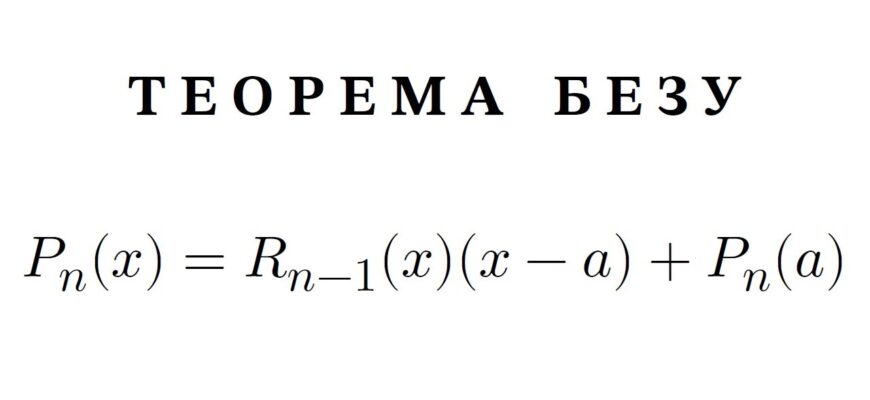Теорема Безу: глибоке розуміння математики
Теорема Безу є важливим математичним принципом, який відіграє істотну роль у теорії многочленів. Вона надає нам можливість глибше зрозуміти властивості і поведінку многочленів шляхом розділення багаторазового поділу залишком.
Що таке теорема Безу?
Теорема Безу стверджує, що якщо многочлен P(x) ділиться на (x – a) з залишком, то значення цього залишку дорівнює P(a). Іншими словами, щоб дізнатись залишок від ділення многочлена на лінійний двочлен, достатньо підставити a в P(x).
Формальне визначення
Нехай P(x) — це многочлен з коефіцієнтами з певного поля. Теорема Безу стверджує, що:
- При діленні P(x) на (x – a), існують такі многочлен Q(x) і залишок r, що:
- P(x) = (x – a)Q(x) + r
- Де r є числовим значенням, або, P(a) = r.
Застосування та наслідки
Швидка перевірка коренів
Теорема Безу забезпечує зручний метод для перевірки, чи є a коренем многочлена P(x). Якщо залишок r дорівнює нулю, тоді (x – a) є точним дільником P(x), тобто a — корінь.
Факторизація многочленів
Ця теорема дозволяє швидше визначити наявність простих лінійних множників у більш складних многочленах за умови, якщо а розв’язує багаторазове підстановлення в P(x).
Ефективні методи обчислень
- Схема Горнера: Удосконалення базової форми теореми Безу для розрахунку значень многочленів з постійними коефіцієнтами. Це значно скорочує обчислювальні витрати.
- Наближені обчислення: Теорема Безу також використовується для обчислення наближених значень коренів через застосування численних методів, таких як метод Ньютона.
Приклад
Розглянемо багаторазовий поділ для P(x) = x3 – 4x2 + 7x – 10 і дільник (x – 2):
| Многочлен | Дільник | Результат |
|---|---|---|
| P(x) = x3 – 4x2 + 7x – 10 | x – 2 | a = 2 |
Замінивши a на 2 в P(x), отримаємо^:
- P(2) = (2)3 – 4(2)2 + 7(2) – 10 = 8 – 16 + 14 – 10 = -4
Тому залишок дорівнює -4, що означає, що (x – 2) не є множником P(x).
Теорема Безу надає нам потужний інструмент аналізу і дослідження многочленів. Вона є не тільки зручним засобом для перевірки, але й фундаментом для багатьох математичних методик. Її логічна простота робить її ідеальною для навчальних завдань та досліджень, тим самим сприяючи подальшому розширенню математичної грамотності та розуміння.