Теорема про суму кутів трикутника
Теорема про суму кутів трикутника є фундаментальним твердженням у геометрії, яке стверджує, що сума внутрішніх кутів будь-якого трикутника у Евклідовому просторі становить 180 градусів. Це базовий принцип, на якому ґрунтується багато інших геометричних концепцій та доведень.
Історія та значення теореми
Теорема про суму кутів трикутника була відома ще у стародавньому світі. Вона є одним з постулатів Евклідової геометрії, яка була описана у «Началах» Евкліда близько 300 року до нашої ери. Цей принцип став незамінним не лише у геометрії, а й у багатьох інших науках та технічних дисциплінах, таких як архітектура, інженерія та астрономія.
Практичне застосування
- У вимірюванні та побудові будівель.
- При проектуванні інфраструктурних об’єктів.
- У розрахунках курсу та навігації.
Доведення теореми
Існує кілька способів доведення теореми про суму кутів трикутника. Розглянемо найпростіше доведення, що базується на властивостях паралельних прямих.
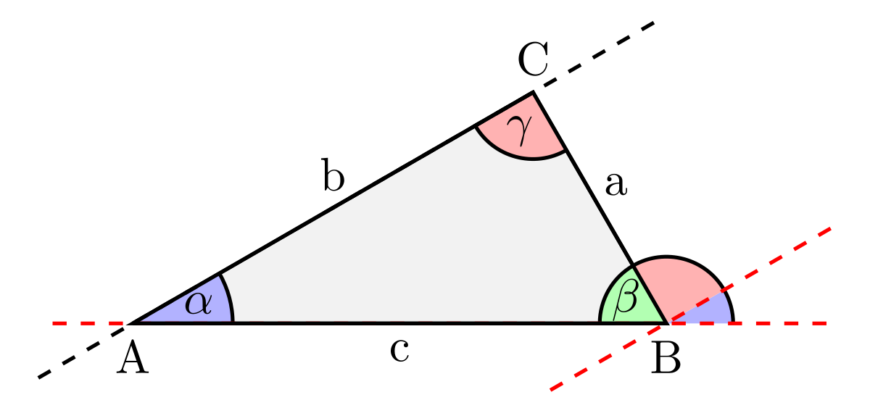
- Нехай у трикутнику ABC внутрішні кути позначаються як α, β, γ.
- Проведемо пряму, паралельну до сторони BC, через вершину A. Ця пряма утворить два допоміжних кути з лініями, що утворюють сторону AC і сторону AB.
- Оскільки пряма паралельна BC, відповідні кути, утворені з α і β, будуть рівними.
- Тепер, сума кутів вздовж прямої — 180 градусів: α’ + β’ + γ = 180°. Звідси α + β + γ = 180°, що і є потрібним твердженням.
Застосування теореми у різних геометріях
Цікаво зазначити, що в неевклідових геометріях, таких як гіперболічна та сферична геометрія, теорема про суму кутів трикутника не виконується у традиційному вигляді.
| Тип геометрії | Сума кутів трикутника |
|---|---|
| Евклідова | 180° |
| Гіперболічна | < 180° |
| Сферична | > 180° |
Гіперболічна геометрія
У гіперболічній геометрії простір викривлений таким чином, що сума кутів трикутника завжди менша за 180 градусів. Це має значення в теорії відносності та вивченні Всесвіту на космологічних масштабах.
Сферична геометрія
На сферичній поверхні, наприклад на земній кулі, сума кутів трикутника може перевищувати 180 градусів. Це важливо для картографів, які створюють навігаційні карти для пілотів та мореплавців.
Висновок
Теорема про суму кутів трикутника залишається наріжним каменем класичної геометрії. Її розуміння дозволяє не лише вирішувати геометричні задачі, але й відкриває доступ до складніших математичних концепцій. Розрізнення поведінки трикутників у різних геометричних площинах демонструє багатогранність і глибину цієї фундаментальної теореми.