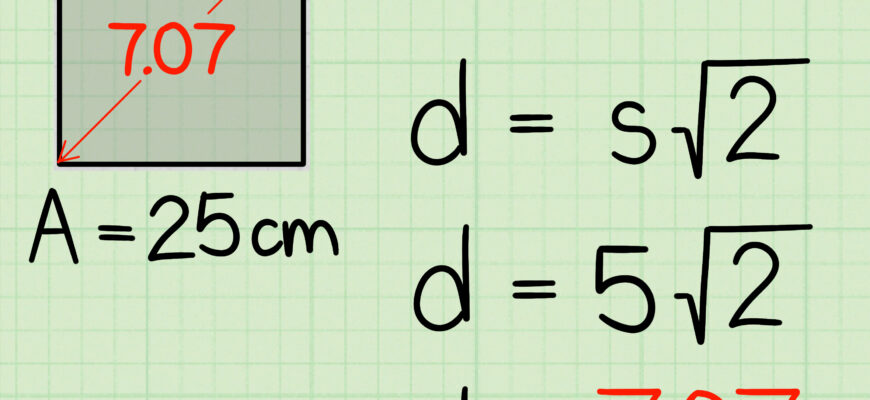Діагональ квадрата: формула та її застосування
Поняття «діагональ квадрата: формула» є важливим аспектом у вивченні геометрії, який часто застосовується в практичних розрахунках. Формула для обчислення діагоналі квадрата дозволяє швидко й ефективно отримати необхідну інформацію про цей геометричний об’єкт, що є основою при вирішенні задач з геометрії, фізики, та інших наук.
Що таке квадрат і чому його діагональ така важлива?
Квадрат – це правильний чотирикутник, де всі сторони рівні, а всі кути прямі. Це особлива форма, яка є основою для багатьох інженерних і архітектурних структур. Діагональ квадрата – це відрізок, що з’єднує дві протилежні вершини. Вона є важливим елементом, оскільки розділяє квадрат на два рівносторонні трикутники і часто використовується для розрахунків в математиці та суміжних дисциплінах.
Формула для обчислення діагоналі квадрата
Діагональ квадрата як знайти? Для цього існує проста і зручна формула:
d = a√2
Де:
- d – довжина діагоналі квадрата,
- a – довжина сторони квадрата.
Ця формула базується на властивостях рівностороннього трикутника, що утворюється діагоналлю квадрата.
Виведення формули
- Розглянемо квадрат з довжиною сторони a.
- Його діагональ поділяє квадрат на два рівносторонні прямокутні трикутники.
- За теоремою Піфагора, квадрат гіпотенузи (діагоналі) дорівнює сумі квадратів інших двох сторін трикутника:
d² = a² + a² = 2a²
Відповідно, довжина діагоналі:
d = √(2a²) = a√2
Приклади використання формули діагоналі квадрата
Практична задача 1:
Обчислити діагональ квадрата, якщо його сторона дорівнює 5 см.
Розв’язок:
d = 5√2 ≈ 7.07 см
Отже, довжина діагоналі цього квадрата – приблизно 7.07 см.
Практична задача 2:
Визначити площу квадрата, якщо його діагональ дорівнює 10 м.
Розв’язок:
| З виразу | d = a√2 |
| Маємо | a = d/√2 = 10/√2 ≈ 7.07 м |
| Площа квадрата | S = a² = (7.07)² ≈ 50 м² |
Таким чином, площа квадрата приблизно дорівнює 50 м².
Важливість знання формули діагоналі квадрата
Знання та вміння застосовувати формулу діагоналі квадрата є незамінним для ефективного вирішення багатьох практичних і теоретичних задач. Така навичка особливо корисна в геометрії, архітектурі та інженерії, де точність розрахунків і простота проведення обчислень мають першочергове значення. Діагональ квадрата формула дозволяє швидко отримати необхідні дані для подальшого аналізу та розрахунків.
Ознайомлення з цією формулою і її застосування на практиці – це фундаментальні кроки на шляху до глибшого розуміння геометричних відносин і властивостей, які закладені в основі багатьох фізичних і математичних теорій.