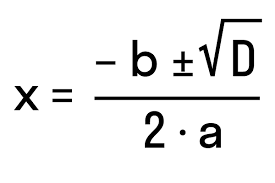Як обчислити дискримінант: формула і приклади розв’язання

Дискримінант Формула: Основи та Застосування

У математиці одним із основних інструментів при розв’язанні квадратних рівнянь є дискримінант формула. Дискримінант допомагає зрозуміти характеристики коренів рівняння без потреби у фактичній їх знахідці. У цій статті ми розглянемо, що таке дискримінант, його важливість та практичне застосування у різних сферах.

Що таке Дискримінант?

Для квадратного рівняння виду:

ax² + bx + c = 0

Дискримінант (D) визначається за формулою:

D = b² – 4ac

Значення дискримінанта допомагає визначити природну характеристику коренів квадратного рівняння:

• D > 0: Рівняння має два різних дійсних кореня.
• D = 0: Рівняння має один дійсний корінь (або коріння співпадають).
• D < 0: Рівняння немає дійсних коренів (існують два комплексних кореня).

Важливість Дискримінанта

Дискримінант формула є ключовою в обчисленні коренів квадратних рівнянь, але її значення виходить за межі чистої математики. Розглянемо кілька її застосувань:

1. Фізика

• Описує рухи об’єктів та розрахунки, пов’язані з законами про падіння тіл.
• Допомагає в аналізі електричних та механічних систем.

2. Інженерія

• Використовується у розв’язанні задач проектування конструкцій.
• Сприяє розробці алгоритмів для моделювання різних процесів.

3. Фінансова аналітика

• Сприяє розрахунку складових економетричних моделей.
• Застосовується для прогнозування та аналізу ризиків.

Застосування Дискримінанта в Розв’язанні Рівнянь

Від обчислення дискримінанта залежить вибір методу розв’язання квадратних рівнянь. Нижче наведено покрокову інструкцію:

1. Обчисліть дискримінант D: Використовуйте формулу b² – 4ac.
2. Аналізуйте значення D: Оцініть його, щоб визначити характеристику коренів.
3. Виберіть підхожий метод розв’язання:
   • Для D > 0 використовуйте формули знаходження двох дійсних коренів:

   Корінь	Формула
   x₁	(-b + √D) / 2a
   x₂	(-b – √D) / 2a

   • Для D = 0 використовуйте формулу:
   • x = -b / 2a
   • Для D < 0 обчисліть комплексні корені:
   • x₁ = (-b + i√|D|) / 2a
   • x₂ = (-b – i√|D|) / 2a

Висновок

Дискримінант формула є невід’ємною частиною математики, допомагаючи швидко та ефективно визначити характеристику коренів квадратних рівнянь. Розуміння і вміле використання формули дискримінанта можуть значно полегшити розв’язання задач у різних наукових та прикладних галузях. Першим кроком до успіху є знання цієї простій формули, яка містить у собі ключ до багатьох математичних дверей.