Формула діагоналі квадрата: Тонкощі та нюанси
Однією з базових геометричних тем є формула діагоналі квадрата. Це поняття допомагає зрозуміти і глибше проникнути у властивості квадрата, однієї з найпростішої і водночас найдосконалішої фігури в геометрії. У цій статті ми розглянемо, як обчислюється діагональ квадрата, яку роль відіграє ця формула в математиці та як її застосовувати на практиці.
Основи розрахунку: що таке діагональ квадрата?
Діагональ квадрата – це відрізок, що з’єднує дві протилежні вершини квадрата. Особливість квадрата полягає в тому, що всі сторони цієї фігури рівні, а кути прямі – по 90 градусів. Це надає діагоналі певні властивості, які є досить унікальними.
Виведення формули діагоналі квадрата
Для того, щоб зрозуміти, як вивести формулу діагоналі квадрата, потрібно скористатися теоремою Піфагора, яка постулює, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. У випадку квадрата, гіпотенузою є діагональ, а катетами – дві його сторони.
- Нехай сторона квадрата дорівнює a.
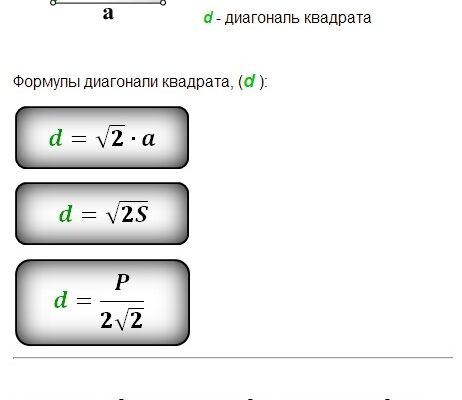
- Тоді, діагональ d квадрата може бути знайдена за формулою: d = a√2.
Цей вираз отримано завдяки тому, що в прямокутному трикутнику, утвореному діагоналлю, кут між сторонами становить 45 градусів, тому діагональ можна записати як корінь з суми квадратів сторін.
Приклад застосування формули
- Візьмемо квадрат зі стороною a = 5 см.
- Використовуючи формулу, обчислюємо діагональ: d = 5√2 ≈ 7.07 см.
- Цей результат ілюструє, наскільки ефективно можна перейти від теоретичного знання до практичного застосування.
Графічне представлення
| Сторона квадрата (a) | Діагональ (d = a√2) |
|---|---|
| 1 | √2 ≈ 1.41 |
| 2 | 2√2 ≈ 2.83 |
| 5 | 5√2 ≈ 7.07 |
| 10 | 10√2 ≈ 14.14 |
Практичне значення та використання
Формула діагоналі квадрата має важливе значення не лише в сфері теоретичної математики, а й у багатьох прикладних галузях. Знання про діагоналі квадрата використовується в архітектурі, інженерії, комп’ютерній графіці та дизайні. Це дозволяє точно розраховувати розміри, раціонально використовувати матеріали і навіть створювати естетичні рішення у вигляді декоративних елементів.
Отже, формула діагоналі квадрата є фундаментальною складовою геометрії з потужним практичним застосуванням і широкими можливостями для досліджень і розрахунків. Застосування її в реальних обставинах робить вивчення математики цікавим і корисним.