Формула площі правильного трикутника
Формула площі правильного трикутника є важливим аспектом вивчення геометрії, оскільки правильний трикутник є однією з фундаментальних форм у планіметрії. У цьому тексті ми детально розглянемо різні підходи до обчислення площі правильного трикутника, дослідимо властивості правильного трикутника та приклади його застосування.
Що таке правильний трикутник?
Правильний трикутник, або рівносторонній трикутник, є спеціальним видом трикутників, у яких усі сторони мають однакову довжину, а всі кути дорівнюють 60 градусів. Це робить його надзвичайно симетричною і гармонійною геометричною фігурою.
Виведення формули площі правильного трикутника
Формулу площі правильного трикутника можна отримати за допомогою різних геометричних підходів. Один з найпростіших методів полягає у використанні формули загальної площі трикутника і тригонометричних функцій.
- Нехай кожна сторона трикутника дорівнює a.
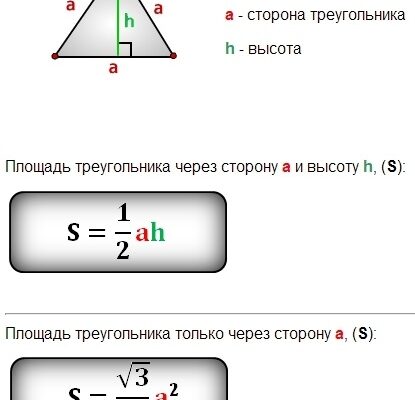
- Висота трикутника може бути знайдена за допомогою формули:
h = (a * √3) / 2. - Знаючи висоту, використовуємо класичну формулу площі трикутника:
S = (a * h) / 2. - Остаточно, підставляємо висоту в формулу площі:
S = (a * (a * √3) / 2) / 2 = (a² * √3) / 4.
Тому, формула площі правильного трикутника виглядає як (a² * √3) / 4.
Переваги та застосування
- **Симетрія**: Завдяки своїй симетрії, правильний трикутник є основою для багатьох декоративних візерунків у архітектурі та дизайні.
- **Будівництво**: Використовується як структурний елемент у будівництві завдяки своїй стійкості.
- **Математичне моделювання**: Правильний трикутник часто використовується в комп’ютерній графіці та моделюванні.
Пояснюючий приклад
Для практичного розуміння формули застосуймо її на прикладі. Припустімо, що у нас є правильний трикутник зі стороною 6 см. Обчислимо його площу:
| Параметр | Обчислення | Результат |
|---|---|---|
| Сторона (a) | 6 см | |
| Формула площі | S = (a² * √3) / 4 | |
| Обчислення | S = (6² * √3) / 4 | |
| Кінцевий результат | ≈ 15.59 см² | 15.59 см² |
Висновок
Формула площі правильного трикутника (a² * √3) / 4 є важливим інструментом для математичних та практичних розрахунків. Розуміння цієї формули дозволяє не тільки вирішувати задачі з геометрії, але і розширити свої знання в математиці та їх застосування у реальному світі.