Як обчислити об’єм і площу конуса: Формула конус для розрахунків

Формула конус: визначення, характеристики та застосування

Формула конус представляє собою набір математичних виразів, що дозволяють обчислити основні параметри цього тіла обертання — об’єм та площу поверхні. Конус — це геометричне тіло, яке утворюється шляхом обертання прямокутного трикутника навколо одного з його катетів. У цій статті ми розглянемо, які формули використовуються для розрахунків, які характеристики конусу є ключовими та як їх правильно застосовувати на практиці.

Основні характеристики конуса

• Основа: Круг у нижній частині конуса, радіус якого позначається як r.
• Висота (h): Відстань від основи до вершини конуса, яка є перпендикулярною до площини основи.
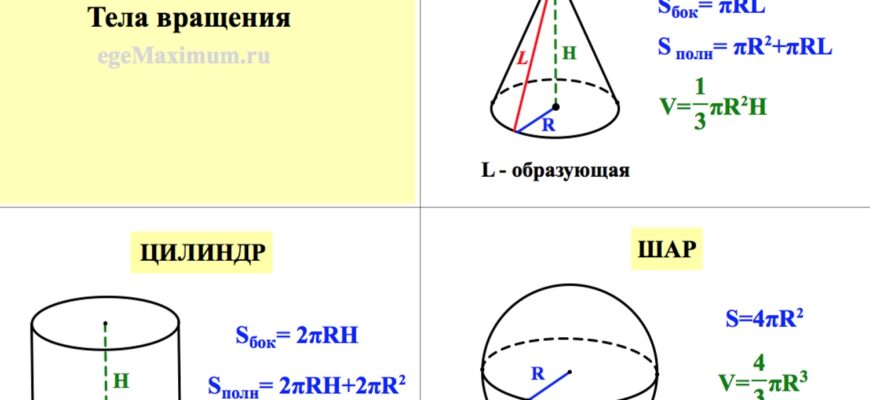
• Утворююча (l): Відстань від вершини конуса до будь-якої точки на колі основи. Це гіпотенуза у сформованому трикутнику, що допомагає визначити нахил.

Формула об’єму конуса

Об’єм конуса можна обчислити, використовуючи наступну формулу:

V = (1/3) * π * r2 * h

Де:

• V — об’єм конуса;
• π — математична константа, приблизно 3.14159;
• r — радіус основи;
• h — висота конуса.

Обчислення площі поверхні конуса

Площа поверхні конуса складається з площі його основи та площі бічної поверхні. Її можна обчислити за допомогою формули:

S = π * r * (r + l)

Де:

• S — повна площа поверхні конуса;
• l — утворююча конуса, яку обчислюють за формулою: l = √(r² + h²);
• Інші елементи формули — такі самі, як і для об’єму.

Приклад розрахунку

1. Нехай радіус основи конуса r дорівнює 4 см, а висота h дорівнює 9 см.
2. Спочатку обчислимо утворюючу l:

    l = √(42 + 92) = √97 ≈ 9.8 см

3. Обчислимо площу поверхні:

    
         S = π * 4 * (4 + 9.8) ≈ 175.75 см2 (з використанням π ≈ 3.14159)
       

4. Об’єм конуса можна визначити наступним чином:

         V = (1/3) * π * 42 * 9 ≈ 150.8 см3
       

Застосування формул конуса

Знання формули конуса корисне в багатьох галузях, включно з інженерією, архітектурою та навіть у повсякденному житті. Наприклад, розрахунок об’єму конуса може знадобитися для визначення об’єму конічних резервуарів, тоді як обчислення площі поверхні може бути ключовим для виготовлення обгорток чи оббивок для конусоподібних об’єктів.

Пам’ятуючи про визначення та правильні формули конуса, ви зможете легко та швидко виконувати всі необхідні розрахунки, що будуть базисом для подальших дій чи проектів. Складність у відображенні та інтеграції точності в розрахунках підкреслює важливість розуміння основ геометрії, що займає важливе місце у повсякденній діяльності людини.