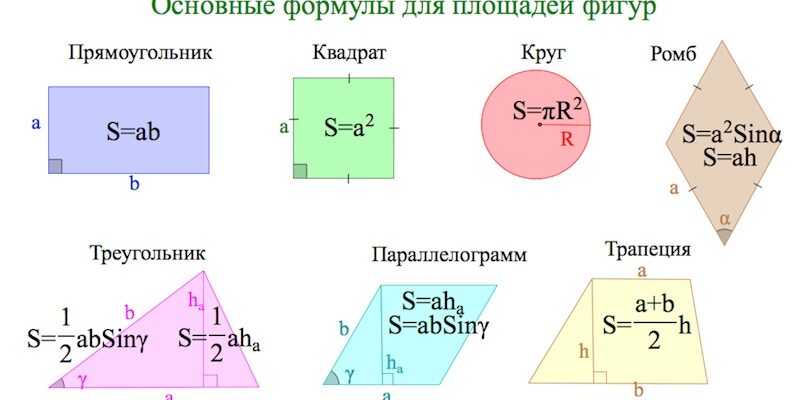
Площа Фомула: Огляд Формул Для Визначення Площі
Тема “площа формула” є однією з основних концепцій у геометрії та математиці, адже через неї учні і студенти отримують можливість вимірювати розмір звичних фігур. Будь-який об’єкт має певну площу, тобто поверхню, яку він займає, і занурення у цю тему дозволить ефективніше розуміти, як взаємодіють різні елементи простору. У цій статті ми розглянемо основні формули для визначення площі різних фігур.
Площа прямокутника
Однією з найпростіших для розуміння формул “площа формула” є формула для обчислення площі прямокутника:
- S = a × b
- де S – площа, a – довжина прямокутника, а b – його ширина.
Ця формула є фундаментальною для багатьох інших обчислень у геометрії.
Площа квадрата
Формула знаходження площі квадрата базується на тому ж принципі, але тільки з урахуванням однаковості сторін:
- S = a²
- де a – довжина сторони квадрата.
Площа трикутника
Трикутники зустрічаються у повсякденному житті значно частіше, ніж здається на перший погляд. Формула для обчислення площі трикутника:
- S = (a × h) / 2
- де a – основа трикутника, а h – висота, проведена до цієї основи.
Площа паралелограма
Формула для знаходження площі паралелограма схожа до площі трикутника, але використовує повну висоту:
- S = a × h
- де a – основа паралелограма, h – перпендикулярна висота.
Площа кола
Неможливо уявити геометрію без круга. Ось формула обчислення його площі:
- S = π × r²
- де r – радіус кола, а π – математична константа, приблизно рівна 3.14159.
Застосування Формул у Практиці
Знання цих базових формул дозволяє успішно вирішувати багато прикладних задач в реальному світі. Наприклад, при побудові споруд, вимірюванні площ під садівництво чи при створенні маленьких дизайнерських проектів, розуміння як застосувати формулу для визначення площі сприяє точнішому результату і оптимізації витрат матеріалів.
Приклад Використання Площі
- Знайдіть площу прямокутного саду з розмірами 10 м на 5 м. Використовуючи формулу S = a × b, отримаємо S = 10 × 5 = 50 м².
- Визначте площу кухонного квадрата зі стороною 4 м. Використовуючи S = a², отримаємо S = 4² = 16 м².
| Фігура | Формула Площі |
|---|---|
| Прямокутник | S = a × b |
| Квадрат | S = a² |
| Трикутник | S = (a × h) / 2 |
| Паралелограм | S = a × h |
| Коло | S = π × r² |
У кінцевому підсумку, розуміння і вміння застосувати правильну “площа формула” для кожного випадку є одним із базових компонентів математики та геометрії, що дозволяє не лише вирішувати академічні задачі, а й більш ефективно підходити до реальних викликів. Наступного разу, коли ви стикнетеся з необхідністю виміряти площу, згадайте ці формули, які значно полегшать вашу роботу.