Площа квадрата: Формула розрахунку та приклади використання
Площа квадрата формула є однією з найпростіших та найосновніших концепцій у геометрії, яка дозволяє нам швидко обчислити величину площини, обмежену чотирма рівними сторонами. У цій статті ми розглянемо способи обчислення площі квадрата та їх застосування на практиці.
Основні поняття
Квадрат — це чотирикутник, в якого всі сторони однакової довжини, а всі кути є прямими. Завдяки цим властивостям, обчислення площі квадрата є доволі простим завданням.
Формула для обчислення площі квадрата
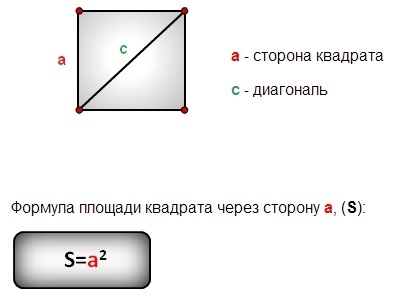
Площа квадрата, формула для обчислення якої є дуже простою, визначається як добуток довжини однієї його сторони на саму себе. Це робить розрахунок площі дуже зручним, оскільки потрібно знати лише довжину однієї сторони:
S = a * a = a²
Де:
- S — площа квадрата;
- a — довжина сторони квадрата.
Так як всі сторони квадрата рівні, досить лише одного вимірювання, щоб визначити площу цієї геометричної фігури.
Приклади розрахунків
Розглянемо декілька прикладів обчислення площі квадрата.
- Нехай довжина сторони квадрата становить 5 см. Тоді площа квадрата буде:
- Другий приклад, якщо сторона квадрата дорівнює 10 м, то площа буде:
S = 5 см * 5 см = 25 см²
S = 10 м * 10 м = 100 м²
Переваги використання формули
- Простота і універсальність: формула для площі квадрата дуже проста і універсальна, що робить її незамінною в будівництві, архітектурі, а також у математиці.
- Швидкість розрахунків: знаючи довжину однієї сторони квадрата, можна швидко та без додаткових обчислень знайти його площу.
- Практичність: вміння швидко обчислювати площу квадрата може бути корисним у повсякденному житті та професійній діяльності.
Таблиця прикладів
| Довжина сторони (a) | Площа (S) |
|---|---|
| 3 см | 9 см² |
| 7 м | 49 м² |
| 2 дм | 4 дм² |
| 8 мм | 64 мм² |
Висновок
Площа квадрата формула є одним з найважливіших інструментів у геометрії. Її простота та зручність роблять її надзвичайно корисною для різних застосувань у науці, техніці та повсякденному житті. Розуміння цієї формули дозволяє не тільки виконувати учбові завдання, але й застосовувати отримані знання на практиці, вирішуючи різноманітні технічні та будівельні задачі.