Як обчислити площу повної поверхні конуса: формула та приклади

Формула площі повної поверхні конуса

Формула площі повної поверхні конуса є важливим елементом у вивченні геометричних фігур. Розрахунок цієї площі дає можливість не тільки оцінити розміри конуса, але й застосовувати ці знання у різних практичних ситуаціях, включно з дизайном, архітектурою й інженерією.

Основні елементи конуса

Конус – це геометрична фігура, що утворюється шляхом обертання прямокутного трикутника навколо одного з його катетів. Щоб зрозуміти, як застосовується формула площі повної поверхні конуса, варто звернути увагу на його основні елементи:

• Основа: круг із радіусом r.
• Висота: перпендикулярний відрізок від вершини конуса до центру основи, позначається як h.
• Утворена поверхня (або бічна поверхня): поверхня, що утворюється при обертанні трикутника.

Компоненти площі повної поверхні

Площа повної поверхні конуса складається з двох компонентів:

1. Площа основи: визначається формулою для площі круга S_основи = πr².
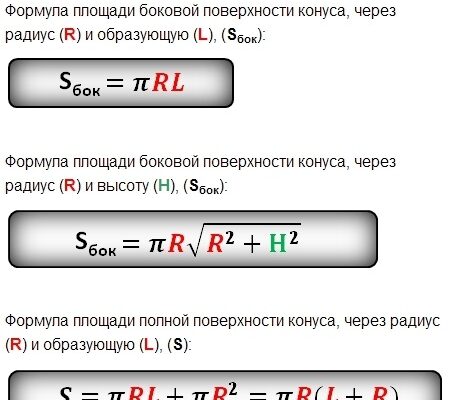
2. Площа бічної поверхні: розраховується за формулою S_бічна = πrl, де l – це довжина твірної конуса, що розраховується за теоремою Піфагора: l = √(r² + h²).

З врахуванням усіх цих компонентів можемо отримати формулу площі повної поверхні конуса:

S = S_основи + S_бічна = πr² + πrl

Приклади застосування формули площі повної поверхні конуса

Формула площі повної поверхні конуса часто використовується у багатьох сферах. Ось декілька прикладів її застосування:

• Архітектура: для проєктування дахів у вигляді конуса, фонтанів та інших архітектурних елементів.
• Інженерія: застосовується при аналізі різних технічних деталей, таких як конічні шестерні.
• Математика і фізика: у обчислювальних задачах, що стосуються об’ємів та поверхонь тіл обертання.

Приклад розрахунку

Розглянемо приклад застосування формули площі повної поверхні конуса. Припустимо, що радіус основи r дорівнює 3 см, а висота h — 4 см. В першу чергу розрахуємо довжину твірної l за теоремою Піфагора:

l = √(3² + 4²) = √(9 + 16) = √25 = 5 см

Тепер можемо розрахувати площу основи та бічної поверхні:

S_основи = π(3)² = 9π см²

S_бічна = π(3)(5) = 15π см²

Отже, площа повної поверхні конуса становитиме:

S = 9π + 15π = 24π см²

Висновок

Формула площі повної поверхні конуса є ключовим інструментом у геометрії, що дозволяє точно визначити розміри та площу цієї фігури. Використовуючи цю формулу на практиці, можна успішно реалізовувати різноманітні завдання в інженерії, архітектурі, дизайні та багатьох інших галузях. Розуміння компонентів і правильне застосування формули є основою для точних і ефективних розрахунків.