Площа прямокутного трикутника: формула обчислення
У геометрії питання, як точно обчислити площу трикутника, завжди є в центрі уваги. Для прямокутного трикутника, найбільш простий і практичний спосіб обчислення полягає у використанні специфічної формули. У цій статті ми детально розглянемо формули для обчислення площі прямокутного трикутника, надамо приклади розрахунків, а також розглянемо основні теоретичні аспекти цього процесу.
Що таке прямокутний трикутник?
Прямокутний трикутник – це трикутник, в якому один з кутів є прямим, тобто дорівнює 90 градусів. Решта два кути в такому трикутнику сумарно складають 90 градусів. Такий тип трикутників відіграє важливу роль не лише в геометрії, але й в тригонометрії, а також у багатьох прикладних науках.
Основна формула для обчислення площі прямокутного трикутника
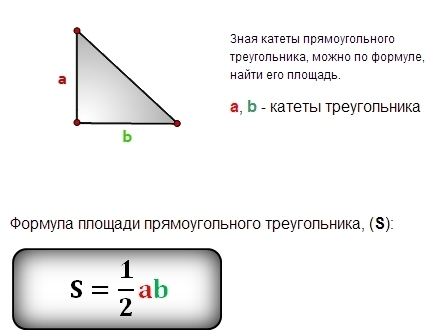
Формула, яку найчастіше використовують для знаходження площі прямокутного трикутника, заснована на добутку довжин катетів, тобто сторін, що утворюють прямий кут. Формула виглядає наступним чином:
S = (a * b) / 2
- a – довжина одного катета
- b – довжина другого катета
Ця формула є дуже ефективною і простою у використанні, оскільки вона дозволяє легко інтегрувати обчислення у більш складні задачі і прикладні застосування.
Переваги використання цієї формули
- Легкість у запам’ятовуванні та обчисленні.
- Широке застосування у багатьох математичних задачах та практичному житті.
- Не вимагає додаткових даних, окрім довжин катетів.
Приклади розрахунку площі
Розглянемо детально кілька прикладів для кращого розуміння.
- Нехай довжина першого катета дорівнює 3 см, а другого – 4 см. Обчислимо площу:
S = (3 см * 4 см) / 2 = 6 см². - Якщо a = 5 см, b = 12 см, тоді площа:
S = (5 см * 12 см) / 2 = 30 см². - При a = 8 см і b = 15 см, отримуємо:
S = (8 см * 15 см) / 2 = 60 см².
Інші методи обчислення площі
Хоча формула площа прямокутного трикутника, заснована на катетах, є найбільш поширеною, існують інші методи обчислення. Наприклад:
| Метод | Опис |
|---|---|
| З гіпотенузою | Використання гіпотенузи і одного катета за допомогою функцій тригонометрії. |
| З радіусом вписаного кола | Використання периметра та радіуса кола, вписаного в трикутник. |
Ці методи можуть бути корисними у випадках, коли додаткові характеристики трикутника вже відомі чи можуть бути обчислені.
Практичне значення формули
Обчислення площі прямокутного трикутника є важливим для багатьох областей: архітектури, інженерії, картографії та багатьох інших. Знання і вміння застосувати цю формулу дозволяє вирішувати широкий спектр задач, що виникають в практичному житті, оскільки прямокутні трикутники часто зустрічаються в різних галузях.