Площа трапеції: формула та застосування
В геометрії часто виникають завдання, які передбачають обчислення площ різних фігур. Однією з таких фігур є трапеція. Площа трапеції: формула — це те, що допомагає дізнатися величину її площі швидко та ефективно.
Що таке трапеція?
Трапеція є чотирикутником, у якого дві протилежні сторони є паралельними. Ці сторони називаються основами трапеції, а інші дві — бічними сторонами.
Формула для обчислення площі трапеції
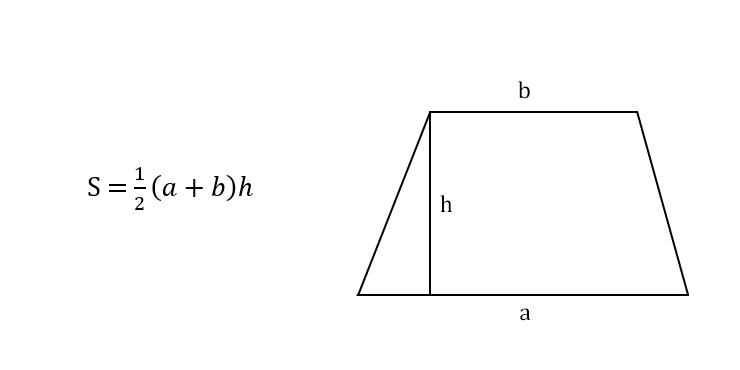
Площа трапеції: формула має вигляд:
Площа (S) = ((a + b) / 2) * h
- a – довжина однієї з основ трапеції;
- b – довжина другої основи трапеції;
- h – висота трапеції, перпендикулярно проведена між основами.
З цією простою формулою можна легко обчислити площу при відомих основах та висоті.
Візуалізація обчислень
| Означення | Позначення | Значення |
|---|---|---|
| Довжина першої основи | a | 6 см |
| Довжина другої основи | b | 4 см |
| Висота | h | 3 см |
| Площа трапеції | S | ((6 + 4) / 2) * 3 = 15 см² |
Використання формули в різних задачах
Нижче наведені приклади, де кожна зі складових формули трапеції знаходиться у різних геометричних задачах:
- Вимірювання спортивних ігрових майданчиків: Великі майданчики, такі як тенісні корти, можуть мати форму трапеції.
- Аналіз архітектурних планів: Трапецієподібні конструкції часто зустрічаються в архітектурі для створення естетично привабливих фасадів.
- Планування садів: У ландшафтному дизайні фігури трапеції використовуються для різноманітності форм ділянок.
Переваги та обмеження
- Переваги: Формула дозволяє швидко та легко розрахувати площу при наявності даних основ і висоти.
- Обмеження: Формула обмежена наявністю прямого вимірювання висоти або можливості її обрахунку через інші методи.
Таким чином, площа трапеції, формула якої стала невід’ємною частиною математичного аналізу, дозволяє вирішувати безліч прикладних завдань у повсякденному житті. Важливо пам’ятати, що правильне використання формули забезпечить точний результат і допоможе у вирішенні різноманітних задач.