Середня лінія трикутника: формула та її значення
Середня лінія трикутника – це ключова тема в геометрії, що часто з’являється як у шкільній програмі, так і в практичних задачах. Формула для обчислення середньої лінії трикутника має важливе значення у розв’язуванні різноманітних геометричних задач.
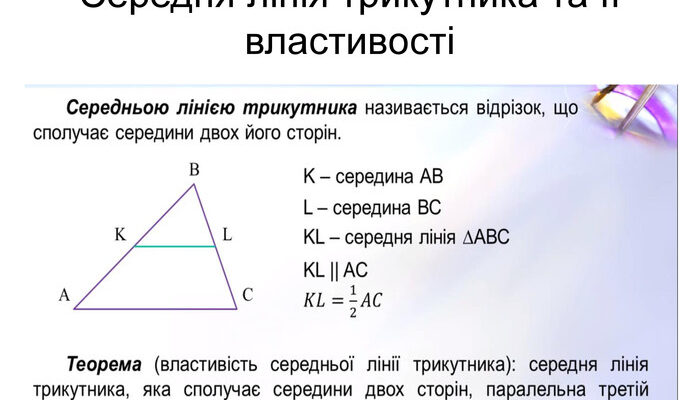
Що таке середня лінія трикутника?
Середня лінія трикутника – це відрізок, що з’єднує середини двох сторін трикутника. Вона має унікальну властивість: середня лінія паралельна третій стороні трикутника і дорівнює половині її довжини. Це фундаментальні властивості, які полегшують розрахунки та забезпечують точність у геометричних доведеннях.
Використання формули середньої лінії
Середня лінія трикутника: формула дозволяє з легкістю знаходити її довжину. Якщо ми маємо трикутник ABC, де середня лінія поєднує точки D і E, які є серединами сторін AB і AC відповідно, то середня лінія DE дорівнює:
- DE = 1/2 * BC
Ця проста формула є надзвичайно корисною в геометричних задачах. З її допомогою можна швидко визначити необхідні відрізки, що спростить розв’язок задач.
Властивості та застосування середньої лінії трикутника
| Властивість | Опис |
|---|---|
| Паралельність | Середня лінія трикутника завжди паралельна третій стороні. |
| Напівдовжина | Довжина середньої лінії становить половину довжини третьої сторони. |
Ці властивості роблять середню лінію важливим інструментом у розв’язанні задач та доведеннях. Вони дозволяють конструювати інші елементи на основі рівноцінних геометричних принципів та легко застосовуються у задачах на побудову.
Приклади використання
- Обчислення координат середньої лінії у координатному трикутнику.
- Побудова та розв’язок трикутників з основними відрізками за допомогою середньої лінії.
- Використання середньої лінії при аналізі властивостей паралелограмів та трапецій.
Таким чином, середня лінія трикутника, формула для її обчислення, є важливим інструментом у вивченні геометрії. Її властивості забезпечують простоту та ефективність у розв’язуванні багатьох практичних задач та у проведенні геометричних досліджень. З досвідом роботи з трикутниками та їх властивостями, така формула стає незамінною у вашому математичному арсеналі.