Вершина параболи: формула та її застосування
В алгебрі та геометрії однією з найбільш важливих кривих для дослідження є парабола. Вершина параболи формула дозволяє визначити ключову точку, яка має велике значення в багатьох галузях математики і суміжних наук. Цей матеріал створений для допомоги в розумінні та застосуванні поняття вершини параболи.
Що таке парабола?
Парабола — це крива, яка формується перетином конічної поверхні з площиною, паралельною її породжуючій лінії. Найпростіша форма параболи може бути описана через квадратичну функцію вигляду:
y = ax² + bx + c,
де a, b, і c — це коефіцієнти, а a ≠ 0.
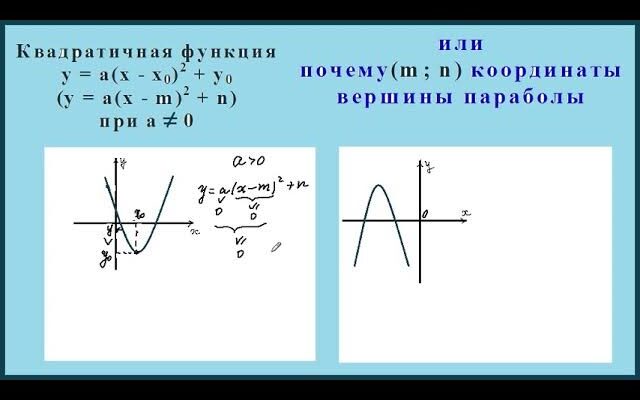
Вершина параболи: визначення
Вершина параболи — це точка, в якій крива робить свій найнижчий або найвищий поворот, залежно від напрямку ветви. Ця точка також може бути розглянута як середина між нулями функції, коли вона існує.
Формула для знаходження вершини параболи
Для квадратичної функції y = ax² + bx + c, вершина параболи може бути визначена за допомогою наступної формули:
- Координата х: x = -b/(2a)
- Координата у: y = f(x) = a(-b/(2a))² + b(-b/(2a)) + c
Недаремно саме ця вершина параболи формула є найефективнішим інструментом для аналітичного знаходження вершини.
Застосування формули вершини параболи
Розглянемо приклад застосування формули:
- Нехай маємо квадратичну функцію y = 2x² – 4x + 1.
- Знайдемо координату x: x = -(-4)/(2*2) = 4/4 = 1.
- Обчислимо координату y: y = 2(1)² – 4(1) + 1 = 2 – 4 + 1 = -1.
Таким чином, вершина параболи має координати (1, -1).
Інші способи опису параболи
Існують інші типи квадратичних функцій, що дозволяють описати параболу, наприклад канонична форма:
y = a(x – h)² + k,
де (h, k) — це координати вершини параболи. Ця форма корисна, коли вершина вже відома.
Таблиця того, на що слід звернути увагу при аналізі параболи
| Елемент | Значення |
|---|---|
| Відкритість параболи | Залежно від знака a: вверх (якщо a > 0) або вниз (якщо a < 0) |
| Координати вершини | Значення (x, y), які визначаються через формулу |
| Симетрія | Відносно осі x = h |
Висновки
Формула для вершини параболи служить важливим інструментом у знаходженні ключових характеристик функції. Вона незамінна для аналітичної геометрії та елементарної алгебри, спрощуючи процес рішення багатьох математичних задач. Розуміння цієї формули відкриває широкі можливості для поглибленого дослідження параболічних функцій у різних наукових та практичних сферах.