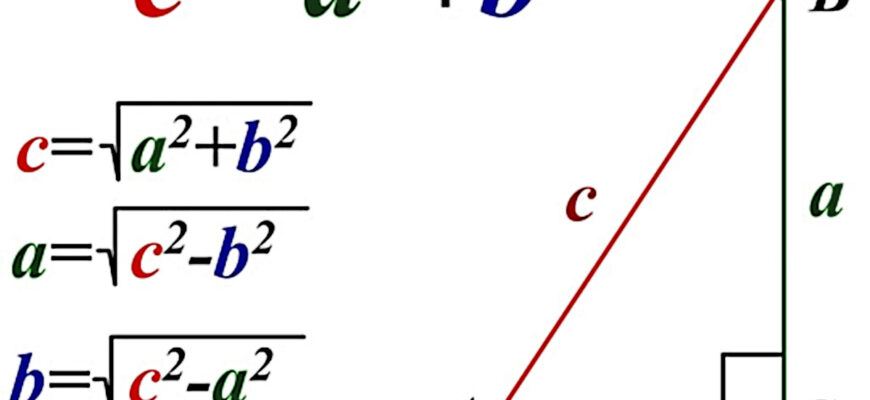Піфагорова теорема: Ключ до геометрії трикутників
Піфагорова теорема є однією з найвідоміших та найчастіше використовуваних у математиці, особливо в геометрії трикутників. Вона формулюється як: у прямокутному трикутнику сума квадратів довжин катетів дорівнює квадрату довжини гіпотенузи. Ця теорема стала основою для багатьох розділів математики та застосовувалася в архітектурі, фізиці і навіть у мистецтві.
Історія та походження
Ім’я теореми походить від давньогрецького мислителя і математика Піфагора, що жив у 6 ст. до н.е. Але існують докази, що принципи цієї теореми були відомі ще до Піфагора в Вавилоні та Індії. Тим не менш, саме Піфагору приписують систематизацію знань цього правила.
Математичне формулювання
Піфагорова теорема може бути записана у вигляді рівняння:
- Для прямокутного трикутника з катетами a і b та гіпотенузою c, формула виглядає так: a2 + b2 = c2.
Доведення теореми
Існує багато способів доведення піфагорової теореми, від алгебраїчних до геометричних. Найбільш поширеним є геометричне доведення з використанням квадратів, побудованих на сторонах трикутника.
- Побудувати прямокутний трикутник ABC, де ∠C = 90°.
- На кожній із сторін трикутника побудувати квадрати.
- Довести, що площа великого квадрата, побудованого на гіпотенузі, дорівнює сумі площ двох менших квадратів, побудованих на катетах.
Застосування в сучасності
Піфагорова теорема має широке застосування в сучасному житті. Від архітектурних проектів до обчислень в рамках GPS-навігації — цей математичний принцип залишається актуальним і корисним.
Приклади застосування:
| Сфера | Приклад |
|---|---|
| Будівництво | Визначення довжин сторін крокв та підкосів у розрахунках дахів. |
| Навігація | Обчислення найкоротших відстаней між точками на площині за допомогою координат. |
| Фізика | Розрахунки векторів сил та швидкостей. |
Заключні думки
Піфагорова теорема залишається одним з фундаментальних принципів математики і геометрії. Її простота і універсальність забезпечують широку сферу застосування, роблячи цей математичний закон не тільки важливим у навчанні, але й незамінним в багатьох професійних галузях. Вивчення та розуміння цієї теореми відкриває двері до глибшого розуміння численних аспектів науки та життя.