Теорема косинусів і синусів: основи та застосування
Теорема косинусів і синусів є фундаментальними елементами у вивченні трикутників у планіметрії, що дозволяють описувати співвідношення між сторонами та кутами.
Основи теореми косинусів
Теорема косинусів є розширенням теореми Піфагора для будь-якого трикутника, будь він прямокутним чи ні. Вона стверджує, що в будь-якому трикутнику ABC, де a, b та c — сторони, а &945;, &946;, &947; — відповідні кути, виконується наступна рівність:
| Формула |
|---|
| c2 = a2 + b2 – 2ab * cos(&947;) |
| a2 = b2 + c2 – 2bc * cos(&945;) |
| b2 = c2 + a2 – 2ca * cos(&946;) |
Ця теорема є надзвичайно корисною для розрахунку довжин сторін трикутника, коли відомі дві сторони та кут між ними.
Застосування теореми синусів
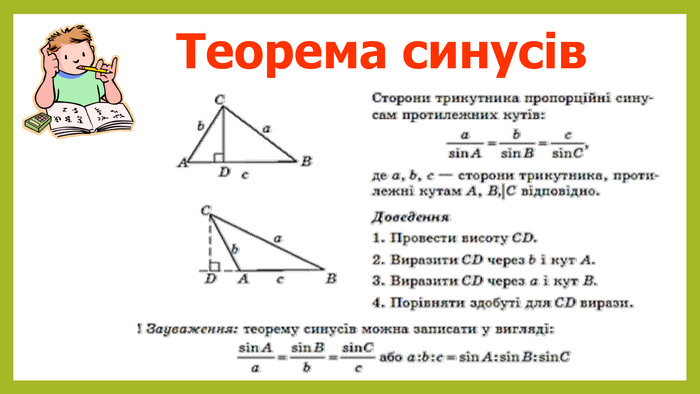
Теорема синусів використовується для визначення співвідношень між сторонами та кутами трикутника. Вона стверджує, що в трикутнику ABC відношення довжини сторони трикутника до синуса протилежного кута є сталою для всіх трьох сторін:
| Формула |
|---|
| a/sin(&945;) = b/sin(&946;) = c/sin(&947;) |
Цю теорему можна застосовувати для обчислення невідомих сторін або кутів у трикутнику, коли відомі дві сторони та не включений між ними кут.
Порівняння та взаємопов’язання теорем
Теорема косинусів і синусів можуть доповнювати одна одну у складних геометричних задачах. Ось кілька сценаріїв, коли їх можна використовувати разом:
- Для обчислення всіх елементів трикутника, коли відомі три сторони.
- Для визначення параметрів трикутника з трьома сторонами, однею з яких є неправильно орієнтована (тобто не між відомими кутами).
- У задачах, де потрібно більше геометричної інформації, ніж можна отримати з однієї лише теоремою.
- Переваги: Насамперед, теорема косинусів дозволяє отримати відсутні значення лише з однією формулою в складних трикутниках.
- Обмеження: Без використання інформації про кути або сторони, неможливо визначити параметри трикутника лише на основі однієї з теорем.
Загалом, теорема косинусів і синусів є надзвичайно потужними інструментами, які допомагають вирішувати широкий спектр задач в прикладній математиці та інших науках. Вони дозволяють глибше зрозуміти співвідношення між компонентами трикутника та зробити точні розрахунки, коли виміри недоступні.