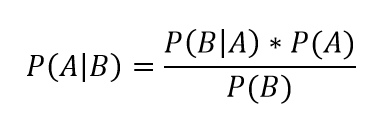Як застосувати теорему Байеса для вирішення практичних задач?

Вступ до Теореми Байеса

Теорема Байеса є одним із наріжних каменів в області статистики, що ґрунтовно змінює спосіб, у який ми аналізуємо дані та приймаємо рішення на їх основі. Вона дозволяє нам знаходити ймовірність настання певної події, враховуючи наявну інформацію, і є особливо корисною в умовах невизначеності та відсутності всіх вихідних даних.

Формулювання Теореми Байеса

Теорема містить математичну формулу, яка дозволяє обчислювати умовні ймовірності. Основне рівняння теореми Байеса має вигляд:

P(A|B) = (P(B|A) * P(A)) / P(B)

Де:

• P(A|B) — ймовірність події A за умови, що подія B вже відбулася.
• P(B|A) — ймовірність події B за умови, що подія A вже відбулася.
• P(A) — ймовірність настання події A.
• P(B) — ймовірність настання події B.

Застосування Теореми Байеса

Області Використання

Теорема Байеса має численні практичні застосування. Деякі з них включають:

• Медична діагностика: для обчислення ймовірностей певних хвороб на основі симптомів пацієнтів.
• Класифікація текстів: у машинному навчанні для аналізу текстових даних і класифікації повідомлень як «спам» або «не спам».
• Фінансовий аналіз: для оцінки ймовірності ринкових трендів.
• Управління ризиками: в економіці і індустрії для оцінки ризиків і прийняття рішень.

Реальний Приклад

Розглянемо простий приклад застосування теореми Байеса в ймовірнісній оцінці:

1. Є захворювання, яке діагностується тестом. Відомо, що ймовірність наявності цього захворювання серед населення становить 1% (тобто P(A) = 0.01).
2. Тест правильно діагностує захворювання у 99% випадків, якщо воно справді є (P(B|A) = 0.99).
3. Проте тест має 5% ймовірність дати хибнопозитивний результат, якщо захворювання насправді немає (P(B|¬A) = 0.05).

Завдання: знайти ймовірність, що тест на захворювання позитивний, враховуючи позитивний результат тесту (P(A|B)).

З допомогою теореми Байеса:

P(A|B) = (P(B|A) * P(A)) / [(P(B|A) * P(A)) + (P(B|¬A) * P(¬A))]

= (0.99 * 0.01) / [(0.99 * 0.01) + (0.05 * 0.99)] ≈ 0.166

Отже, ймовірність наявності захворювання при позитивному тесті складає лише 16.6%.

Висновок

Теорема Байеса є потужним інструментом, що дозволяє перейти від суб’єктивних оцінок до об’єктивних рішень на основі даних. Вона знаходить застосування в різноманітних галузях, від медицини до фінансів, від машинного навчання до управління ризиками. Завдяки своїй універсальності, ця теорема стає незамінною в епоху великих даних.