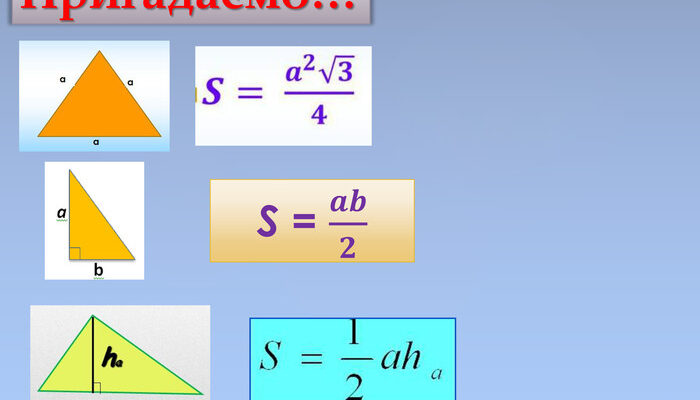
Формула знаходження площі трикутника
Формула знаходження площі трикутника є ключовим аспектом у вивченні геометрії, що допомагає лаконічно визначити площу будь-якого трикутника на площині. Вона має численні застосування як у просторових, так і практичних задачах, допомагаючи зрозуміти конфігурацію та параметри трикутних фігур.
Формули площі трикутника
У геометрії існує кілька формул для знаходження площі трикутника, які можуть застосовуватись в залежності від відомих величин, таких як сторони, висота, кути, радіус вписаного кола тощо. Розглянемо основні з них.
Залежно від відомих елементів
- Базова формула: якщо дана сторона і висота, площа трикутника ( S ) обчислюється за формулою:
Формула ( S = frac{1}{2} times a times h ) де ( a ) – довжина сторони, ( h ) – висота, проведена до цієї сторони.
- Формула Герона: якщо відомі всі три сторони трикутника, площа обчислюється за допомогою напівпериметра:
Формула ( s = frac{a + b + c}{2} ) ( S = sqrt{s times (s-a) times (s-b) times (s-c)} ) - Тригонометрична формула: якщо відомі дві сторони і кут між ними, площа трикутника:
Формула ( S = frac{1}{2} times a times b times sin C ) де ( sin C ) – синус кута між сторонами ( a ) та ( b ).
- Через радіус вписаного кола: якщо відомий радіус вписаного кола ( r ):
Формула ( S = r times s ) де ( s ) – напівпериметр трикутника.
Практичні приклади застосування
- Розрахунок площі будівельних елементів. Часто під час проєктування складних конструкцій, таких як покрівлі, доводиться застосовувати формулу знаходження площі трикутника для точного визначення розміру матеріалу.
- Геодезичні вимірювання. В геодезії для вимірювання земельних ділянок також використовують площі трикутників, особливо коли мова йде про нерівну місцевість.
- Аналіз графічних зображень. Під час роботи з цифровими зображеннями, при обчисленні площ елементів, що мають форму трикутника, актуальною є саме ця формула.
Загалом, формула знаходження площі трикутника залишається одним з найважливіших елементів математики, знаходячи численні застосування в науці, техніці та різних сферах людської діяльності, що робить її вивчення одночасно актуальним та практично корисним.