Формула параллелограмма: основи та застосування
Формула параллелограмма є важливим інструментом у геометрії, який допомагає визначити площу цієї фігури. Це знання корисне як в академічних дослідженнях, так і в повсякденному житті, зокрема в таких галузях як архітектура та інженерія.
Що таке параллелограмм?
Параллелограмм — це чотирикутник, протилежні сторони якого є паралельними. Основною особливістю цієї фігури є те, що протилежні кути рівні, і будь-які дві сусідні сторони утворюють кут, сума якого дорівнює 360 градусам.
Основні формули параллелограмма
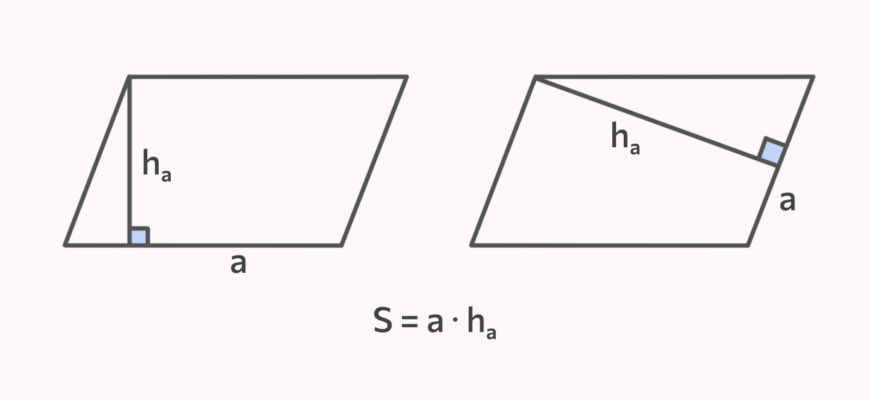
- Формула обчислення площі: Площа (S) параллелограмма дорівнює добутку довжини його основи (a) на висоту (h), проведену до цієї основи. Позначається формулою S = a × h.
- Формула через синус кута: Якщо відомі дві суміжні сторони (a і b) та кут між ними (α), площу можна обчислити за формулою S = a × b × sin(α).
| Елемент | Опис |
|---|---|
| Основи (a, b) | Сторони параллелограма, одна з яких може бути основою у формулах обчислення площі. |
| Висота (h) | Перпендикуляр, що опускається з вершини параллелограма на протилежну сторону або її продовження. |
| Кут (α) | Кут між сторонами a і b. |
Приклади використання формули параллелограмма
- Застосовується в архітектурних розрахунках для визначення необхідного обсягу матеріалу.
- Корисна в комп’ютерній графіці при відображенні тривимірних об’єктів.
- Використовується в фізиці для розрахунку векторних компонентів сил.
Формула параллелограмма є основою для розуміння багатьох складніших просторових структур і обчислень. Знання про те, як використовувати цю формулу, дозволяє ефективно розв’язувати задачі як у навчанні, так і в реальному житті.
Таким чином, опанування формул обчислення площі параллелограмма сприяє розширенню математичної грамотності та вміння застосовувати знання у різноманітних практичних сферах. Розібратися в їх змісті та застосуванні допомагає отримати цілісне розуміння геометрії та її прикладних аспектів.