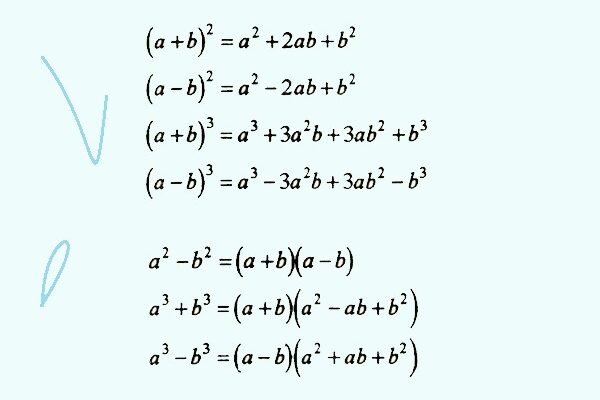Формула алгебра: основи та застосування
Формула алгебра — це невід’ємна частина математичного апарату, який використовується для розв’язання багатьох числових і аналітичних задач. У цій статті ми детально розглянемо основи алгебраїчних формул, їх значення в освітньому процесі та практичному застосуванні.
Що таке формула алгебра?
Формула в алгебрі являє собою математичний вираз, що використовує змінні та математичні операції для опису певного співвідношення чи закономірності. Найпоширеніші формули в алгебрі включають квадратичні рівняння, біноми Ньютона, рівносильні перетворення тощо.
Основні типи алгебраїчних формул
- Квадратична формула: Використовується для розв’язання квадратних рівнянь виду ax2 + bx + c = 0. Її загальний вигляд: x = (-b ± √(b²-4ac))/(2a).
- Формула бінома Ньютона: Описує розкриття степеня суми двох елементів, що виглядає як (a + b)n. Коефіцієнти перед членами визначаються за допомогою трикутника Паскаля.
- Формули скороченого множення: До них відносяться такі формули, як (a+b)² = a² + 2ab + b² та (a-b)² = a² – 2ab + b².
Значення алгебраїчних формул в освіті
Алгебра — це один з головних розділів математики, який вивчається в школах. Формули алгебри є фундаментом для розуміння більш складних математичних концепцій. Учні вчаться розв’язувати рівняння, використовувати функції для моделювання реальних процесів, і в кінцевому підсумку отримують навички критичного мислення та аналітичної обробки даних.
Практичне застосування формул в алгебрі
Формули алгебри знаходять широке застосування не тільки в освіті, а і в реальному житті. Вони використовуються в:
- Інженерії: Застосовуються для обчислень, пов’язаних із будівництвом, механікою, електротехнікою.
- Економіці: Допомагають у фінансовому моделюванні, прогнозуванні витрат і доходів.
- Інформатиці: Алгоритми часто описуються алгебраїчними формулами, що забезпечує ефективність обчислень.
| Тип формули | Застосування |
|---|---|
| Квадратична формула | Розв’язання квадратних рівнянь у фізиці, економіці |
| Біном Ньютона | Комбінаторні задачі, статистика |
| Формули скороченого множення | Спрощення виразів, математичні докази |
Важливість чіткого розуміння формул алгебри
Чітке розуміння і вміння застосовувати формули алгебри дозволяє користуватися цим математичним інструментом не тільки у професійній діяльності, але й у повсякденному житті. Поява проблеми, яку можна виразити математично, чи то фінансова модель чи оптимізація витрат, стає значно простішою для вирішення, якщо ви володієте знаннями з алгебри.
Формули, які ми вивчаємо на шкільних уроках, можуть здатися сухими і абстрактними, але їх практичне значення стає очевидним у реальних умовах. Інтеграція алгебраїчних знань у повсякденність дозволяє підвищити ефективність професійної діяльності і лежить в основі багатьох технологічних процесів. Тому розуміння і застосування формул алгебри є важливим і корисним вмінням.