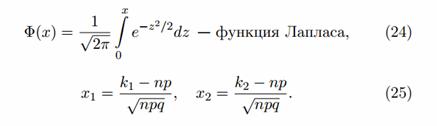Формула Лапласа: Основи та застосування
Формула Лапласа є невід’ємною частиною теорії ймовірностей, яка відіграє важливу роль у математичному моделюванні випадкових процесів. Ця формула дозволяє знаходити наближення для ймовірності того, що сума великої кількості незалежних випадкових величин не перевищить деякого значення. Формула Лапласа заснована на центральній граничній теоремі і широко використовується в статистиці, фізиці, економіці та інших науках.
Історичний контекст
П’єр-Симон Лаплас, французький математик і астроном XVIII століття, зробив істотний внесок у розвиток теорії ймовірностей. Завдяки своїм роботам, Лаплас зміг об’єднати різні погляди на ймовірність, що існували на той час, і розробив численні математичні інструменти для аналізу випадкових явищ. Саме завдяки його зусиллям з’явилася формула, названа на його честь, яка дозволяє прокладати міст між емпіричними спостереженнями та теоретичними ймовірностями.
Формулювання та застосування
Формула Лапласа використовується для наближеного обчислення ймовірностей стандартного нормального розподілу, особливо при великій кількості спостережень. Найчастіше її застосовують у таких сферах:
- Моделювання випадкових процесів у фізиці, зокрема для опису флуктуацій фізичних величин.
- Економічні прогнози, що базуються на статистичних даних великих обсягів.
- Аналітика в соціальних науках, де важливо враховувати варіативність даних.
Математичне пояснення
Формула Лапласа включає нормальне розподілення і стандартну нормальну криву. Найпростіше це можна описати так:
Формула Лапласа: Якщо Y – сума n незалежних випадкових величин з обмеженою дисперсією, то відношення:
P(−a ≤ Y ≤ a) ≈ ∫[−a, a] φ(x) dx, де φ(x) – щільність стандартного нормального розподілу.
Ця формула дозволяє виразити ймовірність Y у термінах площі під кривою нормального розподілу.
Приклад застосування
Для ілюстрації припустимо, що в нас є фабрика, яка виробляє лампочки з середнім часом роботи 1000 годин і стандартним відхиленням 50 годин. Ми хочемо визначити ймовірність того, що середній час роботи 100 лампочок буде між 990 і 1010 годинами. Тут формула Лапласа надає можливість оцінити цю ймовірність, використовуючи нормальний розподіл.
Оцінка та обмеження
Незважаючи на многогранність і корисність, формула Лапласа має свої обмеження. Вона ефективна при великій кількості спостережень, але може бути не точною при невеликих вибірках або якщо випадкові величини мають виражені зміщення чи асиметрію. Важливо враховувати ці фактори при застосуванні формули на практиці.
Висновок
Формула Лапласа являє собою потужний інструмент для аналізу випадкових процесів і використовується в багатьох наукових дослідженнях. Її здатність спростити складні ймовірнісні задачі робить її незамінною у багатьох галузях. Хоча існують певні обмеження, правильне застосування формули відкриває нові горизонти для аналітичних можливостей.