Формула радіуса: Основи та Застосування
Формула радіуса є ключовим елементом в геометрії, особливо у вивченні кола та сфери. Від правильного розуміння та використання цієї формули залежать численні розрахунки, що застосовуються в багатьох галузях науки та техніки. У цій статті ми розглянемо основи формули радіуса, її різновиди, значення та практичне застосування.
Що таке радіус?
Радіус – це відстань від центру кола до будь-якої точки на його периферії. Це базове поняття дозволяє визначити розмір та масштаб геометричної фігури, котра має форму круга або сферу.
Формула радіуса кола
Основна формула радіуса, яка використовується для кола, виражається через співвідношення з довжиною кола (периметром) або площею круга:
| Параметр | Формула |
|---|---|
| Довжина кола (C) | C = 2πr |
| Площа круга (A) | A = πr² |
- Радіус за довжиною кола: r = C / 2π
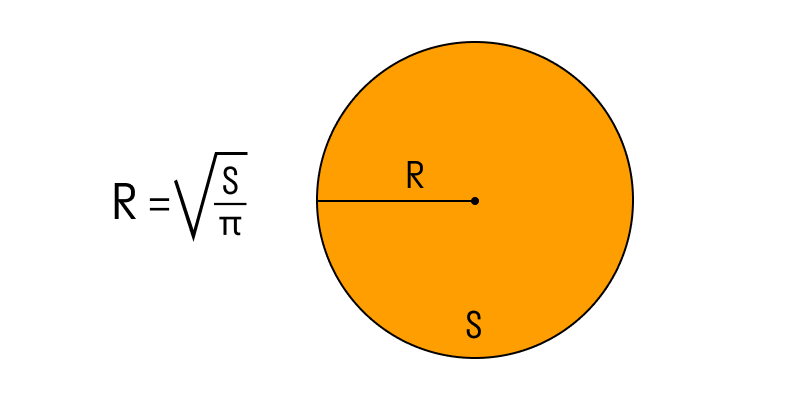
- Радіус за площею круга: r = √(A / π)
Радіус у трьох вимірах: Сфера
У тривимірному просторі радіус використовується для опису сфер. Формули тут дещо відрізняються залежно від того, обчислюється об’єм кулі або її поверхнева площа.
- Поверхнева площа сфери (S): S = 4πr²
- Об’єм сфери (V): V = (4/3)πr³
Виходячи з цих формул, радіус можна обчислити так:
- Радіус за поверхневою площею: r = √(S / 4π)
- Радіус за об’ємом: r = ³√(3V / 4π)
Застосування формули радіуса в повсякденному житті
Формула радіуса застосовується не лише в теоретичній математиці, але й у багатьох практичних ситуаціях:
- Архітектура: Розрахунок вимірів для арок, куполів та інших кругових конструкцій.
- Інженерія: Визначення параметрів труб, кабелів та інших циліндричних об’єктів.
- Астрономія: Вимірювання орбітальних шляхів та розмірів планет і зірок.
Заключні думки
Формула радіуса – це фундаментальний елемент у розумінні та застосуванні геометричних концепцій. Завдяки своїй універсальності та простоті, вона надає змогу ефективно вирішувати широке коло математичних задач, від шкільної геометрії до складних наукових досліджень.