Об’єм конуса: формула і її практичне застосування
Об’єм конуса: формула, котра дозволяє обчислити просторову величину даної фігури, є однією з ключових тем в геометрії та математичному аналізі. У цій статті ми детально розглянемо, як саме можна обчислити об’єм конуса, з’ясуємо, які саме параметри необхідно знати для цього, і розглянемо деякі практичні приклади. Головне завдання – зрозуміти, як ця формула застосовується, і як її можна використовувати у реальних умовах для різних галузей.
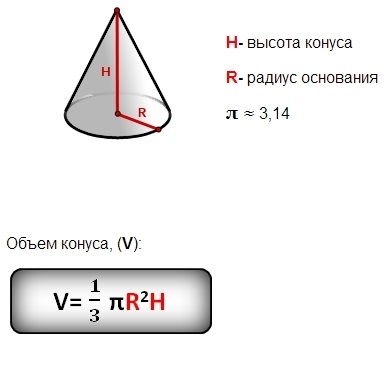
Загальна формула об’єму конуса
Об’єм конуса можна обчислити за допомогою формули:
V = 1/3 π r² h
де:
- V – об’єм конуса;
- π – математична константа, приблизно рівна 3.14159;
- r – радіус основи конуса;
- h – висота конуса (перпендикулярна відстань від основи до вершини).
Компоненти формули
Радіус основи (r)
Радіус – це відстань від центра основи конуса до її периферії. Це важливий параметр, оскільки збільшення радіуса приводить до збільшення площі основи, а, отже, і до збільшення об’єму.
Висота конуса (h)
Висота конуса визначає, наскільки “висока” ця фігура. Чим більше висота, тим більший об’єм за фіксованого радіусу основи.
Значення в реальному світі
Після розгляду теоретичної частини виникає питання: як формула об’єму конуса застосовується на практиці? Нижче – кілька прикладів:
- Інженерія та будівництво: Розрахунок об’єму наповнення конічних силосів або цистерн для рідин чи сипучих матеріалів.
- Мистецтво: Виготовлення фігур та скульптур, особливо якщо вони мають конічні частини.
- Кулінарія: Створення конусоподібних форм для десертів або інших страв.
Покрокове обчислення
Розглянемо приклад обчислення об’єму конуса на практиці:
| Крок | Дія | Результат |
|---|---|---|
| 1. | Знайти радіус основи (r) | r = 5 см |
| 2. | Визначити висоту конуса (h) | h = 12 см |
| 3. | Підставити значення у формулу | V = 1/3 π (5)² (12) |
| 4. | Виконати обчислення | V = 314.16 см³ |
Таким чином, об’єм конуса в нашому випадку становить 314.16 кубічних сантиметрів.
Висновок
Формула об’єму конуса V = 1/3 π r² h є невід’ємною частиною геометрії і знайшла своє застосування в багатьох практичних галузях. Знання про те, як обчислювати об’єм конуса, дозволяє не лише вирішувати різноманітні задачі в сфері освіти та науки, але і дає змогу знаходити технічні рішення у повсякденному житті. Освоєння цієї математичної концепції є корисним навичком, котрий розширює світогляд і надає інструментарій для аналітичного мислення.