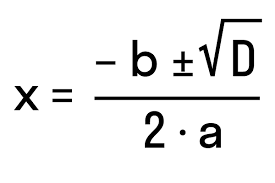Формула дискримінанту: Важливий інструмент в алгебрі
Формула дискримінанту є ключовим елементом в розв’язанні квадратних рівнянь та аналізі їх особливостей. Цей показник дозволяє визначити кількість та природу коренів квадратного рівняння, яке має вигляд ax2 + bx + c = 0. Знання та розуміння дискримінанту є обов’язковими для тих, хто прагне опанувати основи алгебри.
Що таке дискримінант?
Дискримінант, позначений як D, обчислюється за допомогою формули:
D = b2 – 4ac
Використання цієї формули дозволяє знайти важливу інформацію про корені квадратного рівняння. Значення дискримінанту може бути позитивним, нульовим або негативним, причому на кожен з цих випадків припадає свою особливості в характеристиках коренів.
Значення дискримінанту та їх інтерпретація
- D > 0: Коли дискримінант додатний, рівняння має два різних дійсних корені. Це є свідченням того, що парабола, графік даного рівняння, перетинає вісь абсцис в двох різних точках.
- D = 0: Нульове значення дискримінанту свідчить про наявність одного дійсного кореня, або подвійного кореня. Це означає, що вершина параболи торкається осі абсцис.
- D < 0: Від’ємний дискримінант вказує на відсутність дійсних коренів. У цьому випадку корені є комплексними числами і парабола не перетинає вісь абсцис.
Приклад розв’язання квадратного рівняння
Розглянемо приклад квадратного рівняння. Необхідно вирішити рівняння:
2x2 – 4x + 2 = 0
Для цього використаємо формулу дискримінанту:
- a = 2
- b = -4
- c = 2
Підставляємо ці значення в формулу дискримінанту:
D = (-4)2 – 4 * 2 * 2 = 16 – 16 = 0
Оскільки D = 0, рівняння має один подвійний дійсний корінь, який можна обчислити за формулою:
x = -b / 2a = 4 / 4 = 1
Значення і використання дискримінанту
Формула дискримінанту не лише дозволяє встановити кількість і тип коренів, але й надає цінну інформацію для графічного зображення квадратичної функції. Знання про кількість перетинів параболи з віссю абсцис допомагає в аналізі функцій без необхідності їх графічного побудови.
У шкільному курсі математики студенти вивчають формулу дискримінанту як частину фундаменту, на якому ґрунтуються подальші математичні дослідження. У прикладному контексті, розуміння дискримінанту є важливим для інженерів, математиків та в інших технічних спеціальностях.
| Значення D | Кількість коренів | Тип коренів | Графічне зображення |
|---|---|---|---|
| D > 0 | 2 | Різні дійсні | Перетинає вісь абсцис в двох точках |
| D = 0 | 1 | Подвійний дійсний | Дотикається до осі абсцис |
| D < 0 | 0 | Комплексні | Не перетинає вісь абсцис |