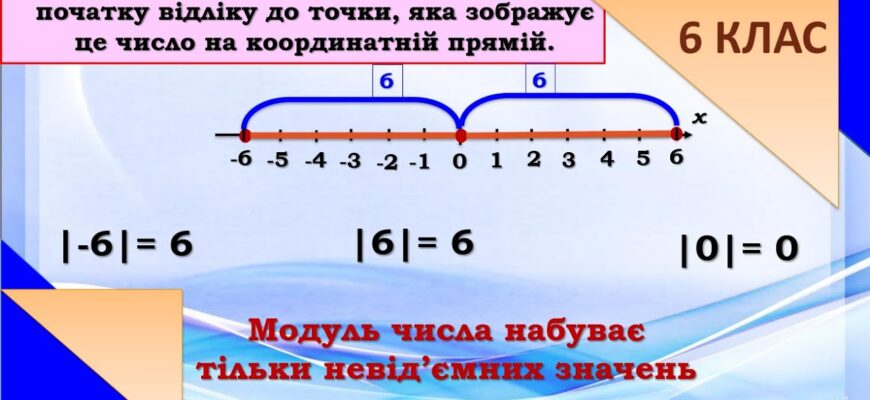
Що таке модуль числа
Що таке модуль числа? У математиці модуль числа, або абсолютна величина, є фундаметальною концепцією, що визначає невід’ємну величину даного числа, незалежно від його знака. Ця величина дозволяє математично оцінити відстань від нуля в числовій системі. Функція модуля числа є елементарним прикладом операцій над числами, і її знання є ключовим для розуміння багатьох інших математичних концепцій, включаючи комплексні числа, вектори та інтеграли.
Визначення модуля числа
Модуль числа позначають вертикальними лініями, наприклад, |x|. Існує два основних правила для визначення модуля:
- Якщо x >= 0, то |x| = x
- Якщо x < 0, то |x| = -x
Інакше кажучи, модуль позитивного числа дорівнює самому числу, тоді як модуль від’ємного числа дорівнює його додатній частині, тобто зміні знака.
Приклади використання
- |5| = 5
- |-3| = 3
- |0| = 0
Властивості модуля числа
| Властивість | Опис |
|---|---|
| Невід’ємність | Завжди |x| >= 0 для будь-якого x. |
| Ідемпотентність | |x| = | |x| | |
| Трикутна нерівність | Для будь-яких x та y, |x + y| <= |x| + |y| |
| Множеннійная властивість | |x * y| = |x| * |y| |
Модуль числа в різних контекстах
Модуль числа застосовується в багатьох розділах математики. Декілька прикладів:
- Комплексні числа: Тут модуль комплексного числа a + bi дорівнює кореню квадратному з a² + b².
- Геометрія: У векторній алгебрі модуль вектора представляє його довжину.
- Аналіз функцій: Властивості абсолютної величини використовуються в багатьох областях, включаючи інтегрування та диференціювання.
Застосування в реальних задачах
Що таке модуль числа у практичних задачах? Його використовують для визначення відстаней на лінії чи площині, а також у багатьох інших сферах:
- Економіка: Застосування модуля для аналізу даних, наприклад, визначення відхилень цін.
- Фізика: При вимірюванні відстаней та інтенсивностей полів.
- Обчислювальна техніка: В обчисленнях, пов’язаних з точністю та відмовостійкістю.
Зрештою, розуміння «що таке модуль числа» є важливим етапом у вивченні математики. Ця концепція не лише надає інструмент для роботи з числами, але й закладає основу для вивчення більш складніших математичних теорій та застосувань. Модуль є універсальною концепцією, що демонструє свою значущість у різноманітних науках та реальних застосуваннях.