Що таке область значень функції?
Область значень функції – це один із фундаментальних концептів в математиці, який відіграє ключову роль у розумінні поведінки функцій. Для початку, щоб зрозуміти, що таке область значень функції, слід згадати, що функція є відображенням з однієї множини (домену) в іншу (кодуомен). Область значень описує множину всіх можливих виходів функції, тобто ті значення, які функція може приймати у результаті виконання свого правила на допустимих входах.
Матеріалізація поняття області значень функції
- Домен функції – це множина всіх можливих вхідних значень, для яких функція визначена.
- Кодуомен функції – це теоретично можлива множина значень, до якої належать виходи функції.
- Область значень функції – це власне множина всіх реальних вихідних значень, які функція отримує при застосуванні до всіх можливих входів з домену.
Як визначити область значень?
Визначення області значень функції є суттєвим завданням в математичному аналізі та алгебрі. Існує декілька різних методів, які можуть бути застосовані.
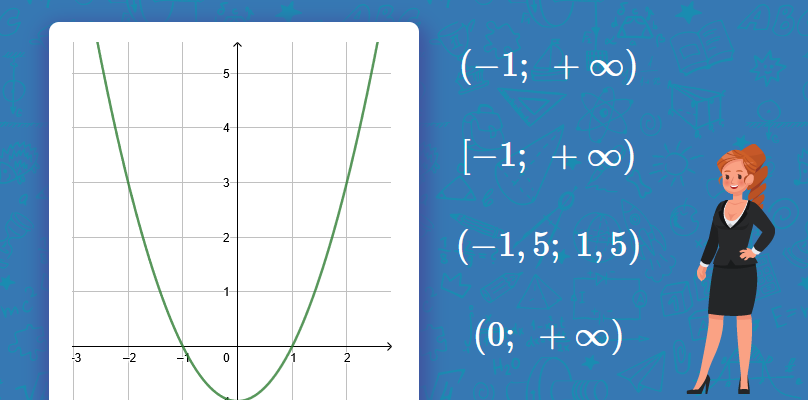
- Графічний метод: Побудувати графік функції та визначити, які значення по осі ординат покриває графік.
- Алгебраїчний метод: Виразити y через x та визначити всі можливі значення y.
- Аналіз за допомогою властивостей функції: Використовувати властивості, такі як монотонність, парність, непарність та періодичність функції.
Приклади
Розглянемо кілька прикладів для кращого розуміння концепту області значень функції.
| Функція | Область значень |
|---|---|
| f(x) = x² | [0, ∞) |
| f(x) = 1/x | (-∞, 0) ∪ (0, ∞) |
| f(x) = sin(x) | [-1, 1] |
Значення області значень функції в прикладних задачах
Розуміння того, що таке область значень функції, допомагає не лише у вирішенні теоретичних математичних задач, але й у численних прикладних ситуаціях. Наприклад, в інженерії та фізиці область значень може визначати допустимі параметри системи або матеріалу. В економіці функції, що описують попит та пропозицію, мають свої області значень, що відображають цінові межі продуктів або послуг.
Часто область значень пов’язується з адаптацією моделі до даних реального світу, де кожна функція може мати обмеження, що відображають реальні фізичні, економічні чи інші властивості. Здатність визначити та інтерпретувати область значень допомагає уникнути помилок у прогнозах, оптимізації та інших аналітичних задачах.