Площа ромба: формули, методи обчислення та їх практичне застосування
Площа ромба, формула якої часто використовується в геометрії та багатьох інших науках, є важливим елементом у розрахунках різноманітних задач. У цій статті ми докладно розглянемо, як обчислити площу ромба, використовуючи різноманітні підходи та формули.
Що таке ромб?
Ромб — це чотирикутник, у якого всі сторони рівні за довжиною. Це робить ромб особливим видом паралелограма. Хоча кути ромба можуть бути різними, його характерною особливістю є те, що протилежні кути завжди рівні.
Властивості ромба
- Всі сторони рівні.
- Протилежні кути рівні.
- Діагоналі перетинаються під прямим кутом.
- Діагоналі ділять кути навпіл.
Формули для обчислення площі ромба
Існують кілька різних формул, які дозволяють обчислити площу ромба, кожна з яких може бути корисною в залежності від наявних даних.
Площа через діагоналі
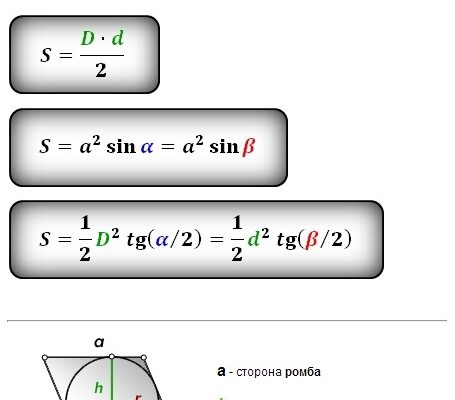
Формула: S = (d1 * d2) / 2
Ця формула базується на використанні довжин діагоналей (d1 і d2), які перетинаються під прямим кутом.
Площа через сторону та висоту
Формула: S = a * h
Ця формула передбачає знання сторони ромба a та висоти h, опущеної на цю сторону.
Площа через сторону та кут
Формула: S = a² * sin(α)
Ця формула використовується, коли відома довжина сторони a та будь-якого внутрішнього кута α.
Застосування формул на практиці
Вибір формули для обчислення площі залежить від умов, що задані в задачі. Розглянемо деякі типові ситуації:
- Якщо відомі діагоналі. У цьому випадку найбільш доречно використовувати формулу через діагоналі. Значення діагоналей можуть бути отримані різноманітними способами, зокрема за допомогою координат геометричних точок.
- Якщо відомі сторона та висота. Це типово для задач, де висота вже прорахована або може бути легко виміряна, наприклад, в архітектурі чи кресленні.
- Якщо відомий внутрішній кут. Формула з використанням синуса кута є достатньо універсальною, оскільки кути ромба можна обчислити з високою точністю.
| Умова | Рекомендована формула |
|---|---|
| Діагоналі відомі | S = (d1 * d2) / 2 |
| Відома сторона і висота | S = a * h |
| Відома сторона і кут | S = a² * sin(α) |
Заключення
Таким чином, площа ромба, формула якої може бути обчислена кількома способами, залежить від конкретних умов задачі. Розуміння та вміння застосовувати правильні формули є критично важливими для успішного вирішення геометричних та прикладних проблем, що дає змогу максимально ефективно використовувати цей математичний об’єкт у різних сферах життя.