Формула косинусів: Основи та практичне застосування
Формула косинусів є одним з фундаментальних принципів тригонометрії, яка надає можливість вирішувати задачі на обчислення сторін і кутів в трикутниках. Це особливо корисно там, де класичні правила прямокутних трикутників не працюють. Оскільки тригонометрія є центральною компонентою математичного аналізу та фізики, важливо розуміти, як і коли використовувати цю формулу.
Що таке формула косинусів?
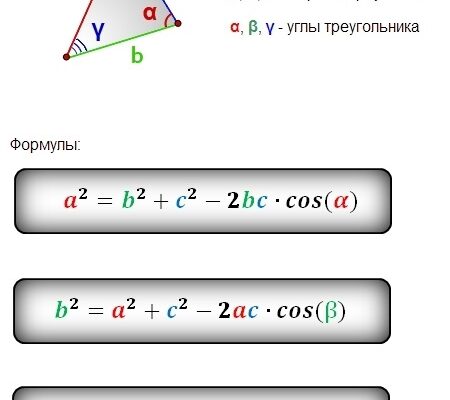
Формула косинусів – це рівність, яка пов’язує сторони трикутника з косинусами його кутів. Для будь-якого трикутника з сторонами a, b, c та кутами A, B, C, формула косинусів для сторони c виглядає наступним чином:
| c² = a² + b² – 2ab * cos(C) |
Залежно від того, яку сторону чи кут потрібно знайти, формулу можна переписати для інших сторін:
- a² = b² + c² – 2bc * cos(A)
- b² = a² + c² – 2ac * cos(B)
Порівняння з теоремою Піфагора
На перший погляд, формула косинусів схожа на теорему Піфагора, яка застосовується в прямокутних трикутниках:
| c² = a² + b² |
Відмінність полягає в додатковому члені -2ab * cos(C), який компенсує нахил сторін у не прямокутних трикутниках. Власне, коли кут C дорівнює 90°, косинус кута дорівнює 0, і формула косинусів перетворюється на теорему Піфагора.
Застосування формули косинусів
Формула косинусів широко застосовується в різних математичних і фізичних задачах. Ось кілька основних випадків, де вона може бути корисна:
- Обчислення сторін трикутника: Якщо відомі дві сторони трикутника і кут між ними, формула косинусів дозволяє знайти третю сторону.
- Обчислення кутів: Якщо відомі всі три сторони трикутника, формула косинусів може бути застосована для обчислення будь-якого кута трикутника.
- Геодезія та картографія: Формула використовується для визначення відстаней на сферичній поверхні Землі.
- Фізика: У задачах динаміки та статики трикутні діаграми сил часто вимагають обчислення кутів і сторін.
Приклад використання
Розглянемо приклад: У трикутнику ABC відомо, що a = 7 , b = 5, а кут C = 60°. Знайдемо сторону c.
Використовуючи формулу косинусів:
| c² = a² + b² – 2ab * cos(C) = 7² + 5² – 2 * 7 * 5 * cos(60°) |
| c² = 49 + 25 – 70 * 0.5 = 49 + 25 – 35 = 39 |
| c = √39 |
Отже, сторона c ≈ 6.24.
Висновок
Формула косинусів служить важливим інструментом для вирішення складних тригонометричних задач, де звичайні методи не можуть бути застосовані. Розуміння і вміння застосовувати цю формулу дозволяє розширити можливості для вирішення практичних задач в різних наукових та інженерних сферах.