Діагональ Куба: Формула, що Розкриває Геометричні Секрети
Коли ми говоримо про діагональ куба, формула, що допомагає її визначити, є одним з ключових аспектів геометрії просторових фігур. Куб — це особлива фігура в геометрії, адже всі його ребра мають однакову довжину, визначаючи його симетричність і витонченість. Визначення діагоналі куба є важливою складовою для розуміння його структури і використання у різних галузях науки та техніки.
Основи Геометрії Куба
Куб — це спеціальний випадок прямокутного паралелепіпеда, у якому всі грані є квадратами. Він має:
- Шість граней
- Дванадцять ребер
- Вісім вершин
Розуміючи ці базові властивості, ми можемо перейти до дослідження його діагоналей.
Типи Діагоналей у Кубі
У кубі існують два основних типи діагоналей:
- Діагоналі граней: Це більш прості діагоналі, які розташовані на кожній з шести квадратних граней куба. Кожна грань має лише дві діагоналі.
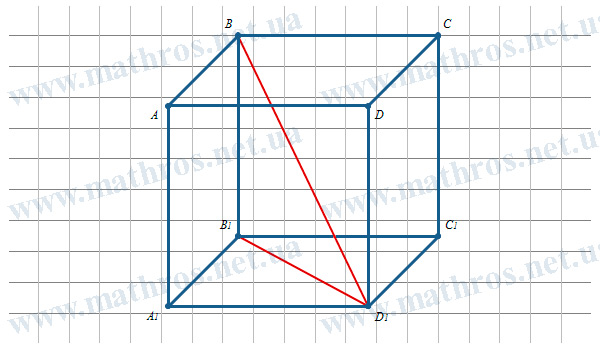
- Просторова діагональ: Діагональ, яка проходить крізь центр куба, з’єднуючи дві протилежні вершини.
Формула для Визначення Діагоналі Куба
Найбільш цікавою є формула для обчислення просторової діагоналі куба. Отже, якщо ми позначимо довжину ребра куба як a, тоді довжина його просторової діагоналі, згідно з теоремою Піфагора, буде дорівнювати:
Формула: d = a√3
Тут √3 є коренем квадратним з трьох. Це число виникає через необхідність обчислення діагоналі у тривимірному просторі, де участь беруть усі три виміри куба.
Застосування Формули у Практиці
Діагональ куба формула має достатньо широке застосування в різних галузях:
- Архітектура та дизайн: Визначення точних розмірів конструкцій, що містять кубічні елементи.
- Комп’ютерна графіка: В моделюванні та рендерингу об’єктів для ігор, фільмів чи віртуальної реальності.
- Фізика: Розрахунок параметрів кристалічних ґраток та їхньої поведінки під дією різних сил.
Розрахунок Діагоналі та Приклад
Розглянемо приклад з реальними числами:
| Довжина ребра (a) | Довжина діагоналі (d) |
|---|---|
| 5 см | 5√3 см ≈ 8.66 см |
Використовуючи стандартний калькулятор або програмне забезпечення для обчислень, можна з легкістю знайти довжину діагоналі куба для будь-якої вказаної довжини його ребра.
Таким чином, діагональ куба, формула якої була розглянута, є не лише математичною задачею, але й важливим практичним методом, що дозволяє краще розуміти і використати геометричні властивості куба в науці та техніці.