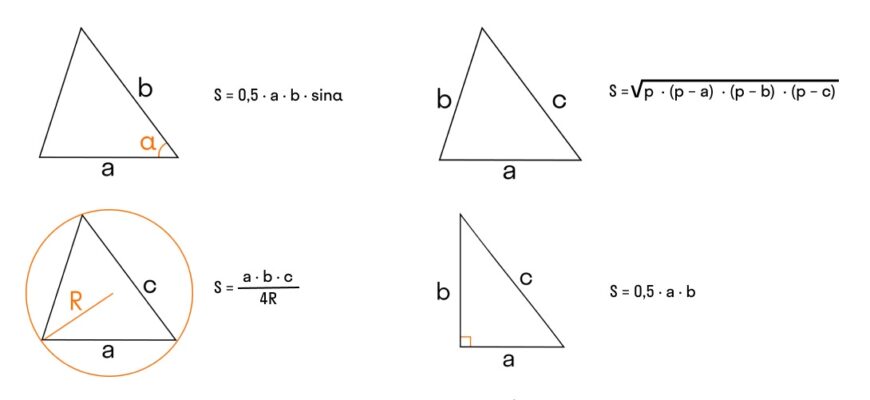
Площа трикутника формула: основні методи обчислення
Площа трикутника формула є однією з ключових тем у вивченні геометрії. У цьому тексті ми розглянемо кілька методів обчислення площі трикутника, які стануть в нагоді за різних умов. Знання цих формул є основою для розв’язання більш складних геометричних задач.
Основна формула: через підставу та висоту
Найпростішою та найвідомішою формулою для обчислення площі трикутника є формула через підставу та висоту. Вона використовується, коли відома довжина підстави трикутника та проведена до цієї підстави висота:
Формула:
P = 0,5 * a * h
де a — довжина підстави трикутника, h — висота, проведена до цієї підстави.
Формула Герона: коли відомі всі сторони
Формула Герона є універсальним методом обчислення площі трикутника, коли відомі всі три його сторони a, b і c:
- Спершу обчислюйте півпериметр s трикутника:
- Далі використовуйте формулу Герона:
s = 0,5 * (a + b + c)
P = √(s * (s - a) * (s - b) * (s - c))
Цей метод є зручним у випадках, коли нехай реалізація інших методів обчислення площі є складною або неможливою.
Площа через кут між сторонами
Ця формула використовується в ситуаціях, коли відомі довжини двох сторін трикутника та кут між ними. Якщо відомі довжини сторін a і b, а кут між ними дорівнює C, площа трикутника обчислюється так:
Формула:
P = 0,5 * a * b * sin(C)
| Метод | Умови використання | Формула |
|---|---|---|
| Через підставу та висоту | Висота відома | P = 0,5 * a * h |
| Формула Герона | Відомі всі сторони | P = √(s * (s – a) * (s – b) * (s – c)) |
| Через кут між сторонами | Відомі дві сторони та кут між ними | P = 0,5 * a * b * sin(C) |
- Тригонометричні методи: Використання тригонометричних функцій, таких як синус, дозволяє знаходити площу за відомими углами та сторонами.
- Алгебраїчні формули: Формула Герона та інші методи, на основі довжин сторін, є алгебраїчними підходами.
Заключення
Таким чином, площа трикутника формула завжди залишається актуальним знанням у математичній освіті, яке відкриває можливості для глибшого розуміння геометрії. Використання різних формул залежить від наявних даних про трикутник та контексту задачі. Маючи в запасі кілька методів обчислення площі трикутника, ви зможете впевнено підходити до розв’язання найрізноманітніших задач. Кожен з описаних підходів має свої переваги і застосовується у відповідних ситуаціях, забезпечуючи точні результати.