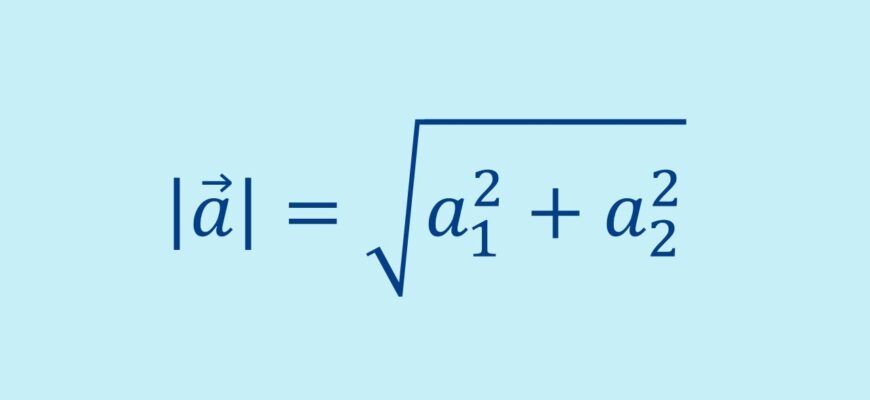Формула модуль вектора: Визначення та Використання
Поняття “формула модуль вектора” є критично важливим у розумінні базових концепцій векторної алгебри, фізики та інших наукових дисциплін, які використовують вектори для моделювання реальних процесів.
Що таке Вектор?
Вектор — це математичний об’єкт, що характеризується як величина, так і напрям. Вектор може бути представлений як стрілка на площині або в тривимірному просторі, де довжина стрілки відповідає його модулю, а напрямок вказує на орієнтацію вектора.
Формула Модуль Вектора
Формула модуль вектора дозволяє обчислити довжину або величину вектора. Для двовимірного вектора (vec{v} = (v_x, v_y)) модуль обчислюється за допомогою формули:
[ |vec{v}| = sqrt{v_x^2 + v_y^2} ]
Для тривимірного вектора (vec{v} = (v_x, v_y, v_z)) ця формула модифікується:
[ |vec{v}| = sqrt{v_x^2 + v_y^2 + v_z^2} ]
Властивості Модуля Вектора
Узагальнену величину вектора можна охарактеризувати наступними важливими властивостями:
- Невід’ємність: ( |vec{v}| geq 0 ). Довжина вектора завжди позитивна або нуль, оскільки корінь квадратний завжди дає невід’ємне значення.
- Нульовий вектор: Модуль нульового вектора дорівнює нулю: ( |vec{0}| = 0 ).
- Одинакова довжина у протилежних векторів: Вектори (vec{v}) і (-vec{v}) мають однаковий модуль.
- Лінійна зміна: Якщо вектор помножити на скаляр, його модуль змінюється згідно зі зміною скаляра: ( |cvec{v}| = |c||vec{v}| ).
Застосування Формули Модуля
Модуль вектора знаходить застосування в різних галузях, таких як:
- Механіка: Визначення скалярних величин, таких як швидкість або сила.
- Електрика та магнетизм: Обрахунок електромагнітних полів і напруженостей.
- Комп’ютерна графіка: Нормалізація векторів для визначення напрямку без зміни їх довжини.
- Наближення в задачах оптимізації: Використання в алгоритмах машинного навчання.
Таблиця: Формули для Модуля Вектора
| Тип вектора | Формула |
|---|---|
| Двовимірний вектор | (|vec{v}| = sqrt{v_x^2 + v_y^2}) |
| Тривимірний вектор | (|vec{v}| = sqrt{v_x^2 + v_y^2 + v_z^2}) |
Підсумок
Формула модуль вектора є основоположним інструментом для аналізу і розуміння векторів у багатьох наукових дисциплінах. Її універсальність і простота роблять її незамінним елементом як у теоретичних дослідженнях, так і в практичних застосуваннях для оцінки та розв’язання завдань.