Площа рівнобедреного трикутника: формули та приклади
У геометрії рівнобедрений трикутник займає особливе місце завдяки своїм унікальним властивостям. Навчаючись обчислювати його площу, важливо знати як базові, так і специфічні формули. Площа рівнобедреного трикутника формула є основою для розв’язання багатьох геометричних завдань.
Властивості рівнобедреного трикутника
Рівнобедрений трикутник характеризується наявністю двох сторін однакової довжини, які називаються бічними сторонами, і третьої основи. Типовими властивостями є:
- Одинакові кути між основою та бічними сторонами.
- Перпендикуляр, проведений з вершини, ділить трикутник на два рівнобедрених прямокутних трикутника.
Формули для обчислення площі
Основна формула площі трикутника
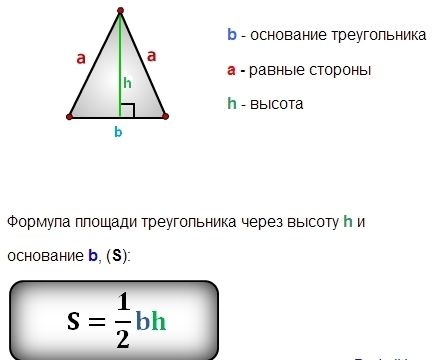
Перш ніж перейти до специфічних формул, важливо знати класичну формулу площі трикутника:
- S = 0.5 * a * h,
де S — площа трикутника, a — довжина основи трикутника, h — висота від вершини до основи.
Формула Герона
Формула Герона дозволяє знайти площу трикутника за трьома сторонами. Для рівнобедреного трикутника вона виглядає наступним чином:
- S = √(p*(p-a)*(p-b)*(p-b)),
де p — півпериметр трикутника, обчислюється як (a + 2b) / 2, a — основа, b — бічна сторона.
Формула з використанням синуса
Існує ще одна зручна формула для обчислення площі з використанням кута між бічними сторонами:
- S = 0.5 * b2 * sin(α),
де b — бічна сторона, α — кут між бічними сторонами.
Формула через апофему
Апофема — це відрізок, який сполучає вершину трикутника з основою, дорівнює половині довжини основи, на яку опущено перпендикуляр. Вона також допомагає знайти площу:
- S = b * a0,
де a0 — апофема.
Приклад обчислення площі рівнобедреного трикутника
Розглянемо приклад обчислення площі з використанням різних формул.
| Параметр | Значення |
|---|---|
| Основа (a) | 6 см |
| Бічна сторона (b) | 5 см |
| Кут (α) | 45° |
- За основною формулою: S = 0.5 * 6 * h. Висота (h) обчислюється через діагональ рівнобедреного прямокутного трикутника: h = √(b2 – (a/2)2) = √(25 – 9) = 4 см. Площа: 12 см2.
- За формулою Герона: Півпериметр p = (6 + 5 + 5) / 2 = 8 см. Площа: √(8*2*3*3) = √144 = 12 см2.
- Через синус кута: S = 0.5 * 52 * sin(45°) ≈ 12 см2.
Висновок: Переваги застосування різних формул
Площа рівнобедреного трикутника формула є необхідним інструментом для всіх, хто вивчає геометрію. Різноманітність методів розрахунку площі дозволяє обрати найбільш зручний спосіб в залежності від наявних даних. Таким чином, глибоке розуміння кожної формули забезпечує успішне розв’язання задач, підвищуючи впевненість у використанні геометричних принципів.