Периметр формула: основи розрахунків у геометрії
Периметр формула завжди був важливою частиною навчального процесу в шкільній математичній програмі. Визначення периметру є фундаментальним етапом у вивченні геометрії, і цю концепцію можна застосовувати в багатьох реальних ситуаціях. Периметр — це відстань навколо 2D фігури, і його розуміння є необхідним для вирішення багатьох геометричних задач.
Що таке периметр?
Периметр – це загальна довжина кола навколо геометричної фігури. Це означає, що для будь-якого багатокутника периметр є сумою довжин усіх його сторін. Ця проста концепція лежить в основі розрахунків, пов’язаних з вимірюванням простору.
Периметр формула для різних геометричних фігур
Кожна геометрична фігура має свою унікальну периметр формула, яка базується на характеристиках цієї фігури. Нижче наведені приклади формул для обчислення периметру деяких стандартних фігур:
- Квадрат: Для квадрата, де всі сторони рівні, периметр дорівнює 4 помноженому на довжину однієї сторони (P = 4a).
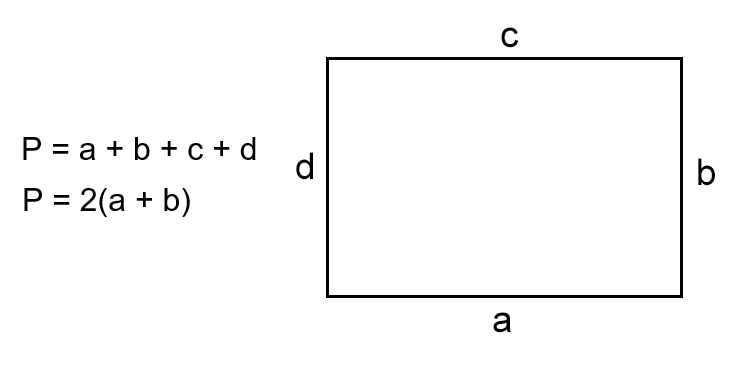
- Прямокутник: Периметр прямокутника обчислюється шляхом додавання довжин обох пар паралельних сторін (P = 2a + 2b).
- Трикутник: У випадку трикутника потрібно скласти всі три сторони (P = a + b + c).
- Коло: Периметр кола, також відомий як окружність, дорівнює добутку діаметра на π (P = 2πr).
Важливість у реальному житті
Знання про те, як обчислити периметр, часто застосовується у практичних завданнях. Наприклад, це може бути корисним при розрахунку кількості матеріалів, необхідних для обробки бордюр чи створення огорожі навколо території.
Таблиця формул для обчислення периметра
| Форма | Периметр формула |
|---|---|
| Квадрат | P = 4a |
| Прямокутник | P = 2a + 2b |
| Трикутник | P = a + b + c |
| Коло | P = 2πr |
Рекомендації для вивчення
- Практика: Регулярне виконання вправ допомагає закріпити знання на практиці та розвиває впевненість у використанні формул.
- Концептуальне розуміння: Розуміння геометричних принципів, які стоять за формулами, дозволяє легше запам’ятовувати та застосовувати їх.
- Застосування у житті: Пошук реальних ситуацій, у яких можна застосувати обчислення периметру, робить навчання більш захоплюючим.
Висновок
Периметр формула є важливою темою в геометрії, яка знаходить багато застосувань і в реальному житті. Навики обчислення периметру допомагають розвивати критичне мислення і розуміння фундаментальних принципів математики. Продовжуйте вивчати та практикувати розрахунки, щоб стати справжнім експертом у цій темі!